Thevenin’s Theorem with solved problem

ByAbragam Siyon Sing Updated on
Thevenin's Theorem

Thevenin’s theorem is used to solve the complex circuits consisting of several sources and impedances by converting them into a simple equivalent circuit called Thevenin’s equivalent circuit. Now let’s look at the statement.

Thevenin’s Theorem states that

“Any linear bilateral circuit containing several voltage sources and impedances can be replaced with an equivalent circuit consisting of single Thevenin’s voltage source in series with a Thevenin’s impedance connected across the load impedance“.

The Thevenin’s equivalent circuit has a single voltage source called Thevenin’s voltage source(VTH), equivalent impedance called Thevenin’s equivalent impedance ZTH and a load impedance ZL.

Thevenin’s Theorem

In the above equivalent circuit, the Thevenin’s voltage VTH is nothing but an open-circuit voltage, which is obtained by removing the load impedance ZL. The Thevenin’s equivalent impedance ZTH is obtained by short-circuiting all the voltage sources and open circuiting all the current sources in the circuit.

Now, let us look at the step-by-step procedure to determine the VTH and ZTH in the above circuit.

Procedure to determine Thevenin’s equivalent circuit

Step 1 – Determination of Thevenin’s Voltage

Remove the load impedance ZL in the above electric circuit, by open circuiting the terminal ab as shown in the below figure.

Step 1 - Determination of VTH

In this circuit, there exists a loop, through which the current I flows. Apply KVL to the loop and find the current I.

    \[I.Z_1 + I.Z_3 = V_s \]

Solving the above equation, we will get the value of current. Then Thevenin’s voltage is obtained for the circuit as,

    \[V_{TH} = I.Z_3 \]

Step 2 – Determination of Thevenin’s Impedance

Since there is only one voltage source is available in the circuit, remove the voltage source and short circuit the terminals and remove the load impedance, as shown in the figure below.

The Thevenin’s equivalent impedance is obtained from terminal ab using the formula,

    \[Z_{TH} = \frac{Z_1 . Z_3}{Z_1 + Z_3} + Z_2 \]

Step 3 – Formation of Thevenin’s equivalent circuit

Using the obtained values of VTH and ZTH, the equivalent circuit is drawn as below. This circuit is called Thevenin’s equivalent circuit.

Step 3 - Formation of Thevenin's equivalent circuit

From this circuit, we can obtain the current flowing through the load, using the formula

    \[I_L = \frac{V_TH}{Z_TH + Z_L}\]

Solved Problem 1

Solve the given circuit to find the current through 10 Ω using Thevenin’s Theorem.

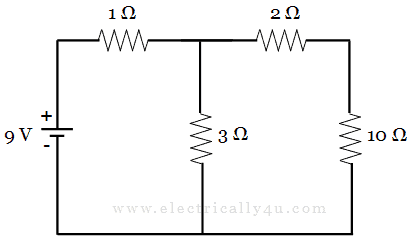
Thevenin’s Theorem - Solved Problem 1

First, let us consider 10 Ω as the load resistor.

(a) To find Thevenin’s voltage, Remove the load resistor(10 Ω) and the circuit is redrawn as below.

Thevenin’s Theorem - Problem_1 solution_1

Now the circuit is open-circuited. From the drawn circuit, Thevenin’s voltage is calculated between a and b. Since no current flows through 2 Ω, VTH is equal to the voltage across 3 Ω resistor.

To find the voltage across the 3 Ω resistor, we need to know the current flowing through it.

The total resistance in the circuit, R = 1 Ω + 3 Ω = 4 Ω.

By Ohm’s law,

    \[I = \frac{V}{R} = \frac{9}{4} = 2.25 A\]

Thus, the voltage across 3 Ω resistor(or Thevenin’s voltage VTH) is given by,

    \[V_{ab} = V_{TH} = I * R = 2.25 * 3 = 6.75 V \]

(b)To find Thevenin’s resistance, Remove the load resistor, short the voltage source and circuit is redrawn as below.

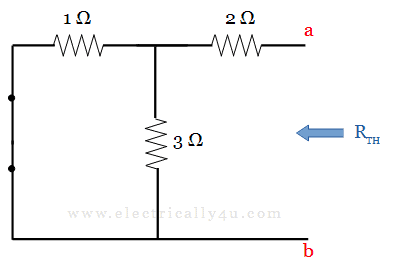
Thevenin’s Theorem - Problem_1 solution_2

In this circuit, we can observe that the 2 Ω resistor is in series with the parallel combination of 1 Ω and 3 Ω resistors. Thus the equivalent value of resistance is obtained as,

    \[R_{TH} = 2 + \frac{1 * 3}{1 + 3} = 2.75 \Omega \]

[Learn how to find the equivalent resistance of resistor when they are connected in series and parallel.]

(c)Thevenin’s Equivalent Circuit. It is drawn by connecting the Thevenin’s voltage VTH, Thevenin’s resistance RTH and load resistor in series, as shown below

From this circuit, IL is the current flowing through the load of 10 Ω resistance.

    \[I_L = \frac{V_{TH}}{R_{TH} + R_L} = \frac{6.75}{2.75 + 10} = 0.529 A \]

Solved Problem 2

Solve the given circuit to find the current through 15 Ω using Thevenin’s Theorem.

Thevenin’s Theorem - Problem_2

In this problem, let us consider 15 Ω resistor as the load.

(a) To find Thevenin’s voltage, Remove the load resistor(15 Ω). Also when observing the circuit, it has 2A current source in parallel with the 5 Ω resistor.

By source transformation, let us convert this current source into its equivalent voltage source in series with 5 Ω resistor.

Thevenin’s Theorem - Problem_2 solution_1

Now we have the following circuit, for which we have to find the Thevenin’s voltage VTH. You can observe a loop in this circuit. [Learn how to solve a circuit using mesh analysis.]

Thevenin’s Theorem - Problem_2 solution_2

Let us apply Kirchoff’s Voltage Law to this loop and find the value of loop current.

Applying KVL, 20I + 5I +10 – 40 = 0

25I = 30

I = 1.2 A

VTH = 10 + (5 * 1.2) = 16 v

(b)To find Thevenin’s resistance, Remove the load resistor, short the voltage source and the circuit is redrawn as below.

Thevenin’s Theorem - Problem_2 solution_3

When you observe the circuit between points a and b, the 5 Ω resistor looks parallel to the 20 Ω resistor. Thus the equivalent value of resistance is obtained as,

    \[R_{TH} = \frac{5 * 20}{5 + 20} = 4 \Omega \]

(c)Thevenin’s Equivalent Circuit. It is drawn by connecting the Thevenin’s voltage VTH, Thevenin’s resistance RTH and load resistor in series, as shown below

Thevenin’s Theorem - Problem_2 solution_4

From this circuit, IL is the current flowing through the load of 10 Ω resistance.

    \[I_L = \frac{V_{TH}}{R_{TH} + R_L} = \frac{16}{4 + 15} = 0.842 A \]

2 Shares

An Assistant Professor in the Department of Electrical and Electronics Engineering, Certified Energy Manager, Photoshop designer, a blogger and Founder of Electrically4u.

Related Posts

Leave a Reply

Your email address will not be published. Required fields are marked *

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

7 Comments

  6. sir how r u calculating vth in problem i am unable to understand sir i am having exam tmw can u help me out we u see this mail

    Reply