Plotting Karnaugh Map with examples
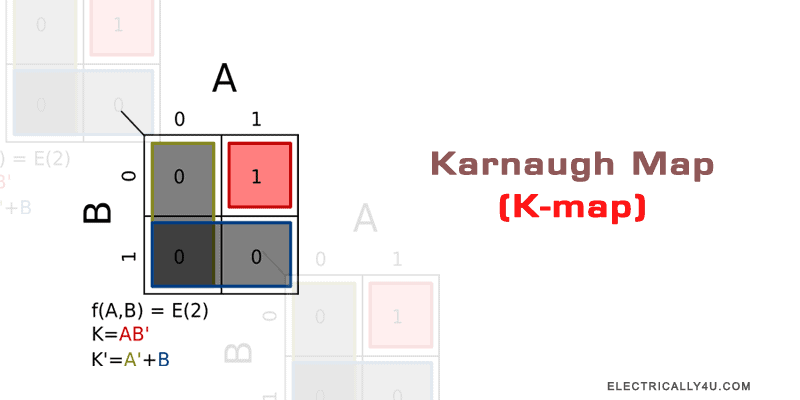
Simplification of Boolean expression by using postulates and theorems of Boolean algebra can never be the simplest possible expression. So we use the Karnaugh map or K map to simplify the boolean expressions.
What is Karnaugh map or K-map?
Karnaugh Map is a systematic approach or map method for simplifying Boolean expressions. It does not require any manipulation using boolean algebra. It was originally introduced by Allan Marquand in the year 1881.
It was rediscovered by Edward Veitch in 1952 and modified by Maurice Karnaugh in 1953. Hence called as Veitch diagram or the Karnaugh map.
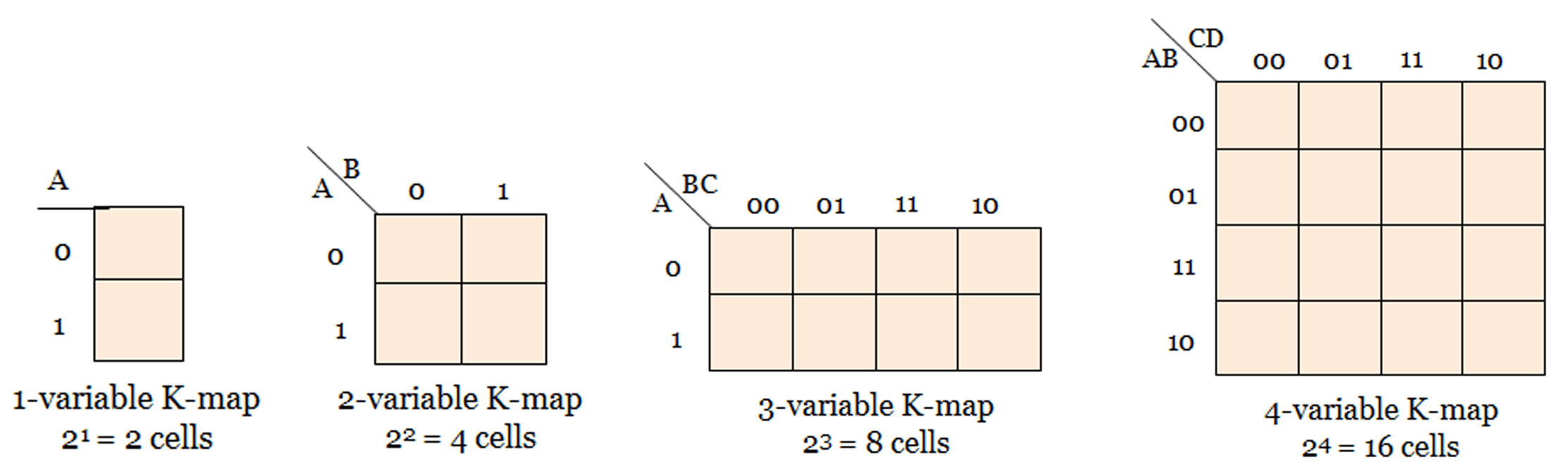
The K map contains boxes called cells. Each cell represents one of the 2n possible terms(either product term or sum term) that can be formed from the number of variables.
For example, for a 2-variable map, there will be 22 = 4 cells, for a 3-variable map, there will be 23 = 8 cells, and so on.
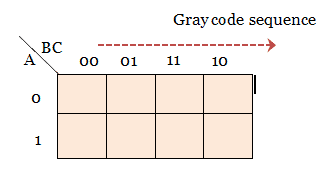
For labeling, when we move from one cell to the next cell along any row or column, only one variable changes to either a complemented form or an uncomplemented form.
In other words, the rows and columns of a K map are labeled by the gray code sequence as shown below.
The product terms or sum terms are assigned to each cell corresponding to the product or the sum of rows and columns of the particular cell. Each cell is numbered from 0 to 7 for an 8-cell K map.
While doing so, cells in the first row are numbered 0, 1, 3, and 2(the number order 2 and 3 are reversed as the labeling follows the gray code sequence 00, 01, 11, and 10).
The cells in the second row are numbered 4, 5, 7, and 6. For a clear understanding, look at the picture below.

In the above diagram, cell 0 has the value AB’C’, which corresponds to the row(A) and column(B’C’) of that cell and cell 1 has the value A’B’C, which corresponds to the row(A) and column(B’C’) of that cell. In the same way, the values of all the cells are written.
Instead of writing the actual product terms in SOP form, the corresponding minterm notations can be written in the cell.
Similarly, instead of labeling the rows and columns with the variable and its complement, they are marked with gray codes.

In the same way, K maps can be used for simplification of the product of sum(POS) form. Instead of writing the actual sum terms in POS form, the corresponding maxterm notations can be written in the cell.

Plotting a Karnaugh Map
A logic function either in a truth table format, SOP expression, or POS expression format can be easily plotted in karnaugh maps.
Each K-map is the extended version of truth tables, in which the K-map representation follows a different approach.
Let us look at the procedure to plot. Here the plotting of 4 cells K-map and 8 cells K-map is shown for your understanding purpose.
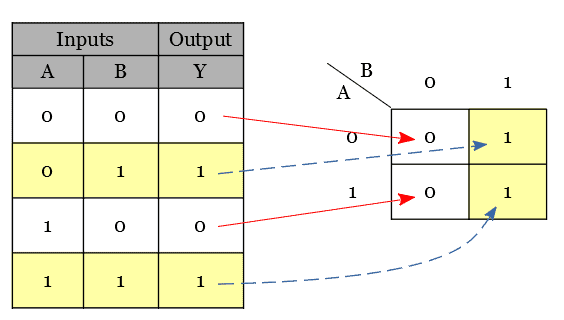
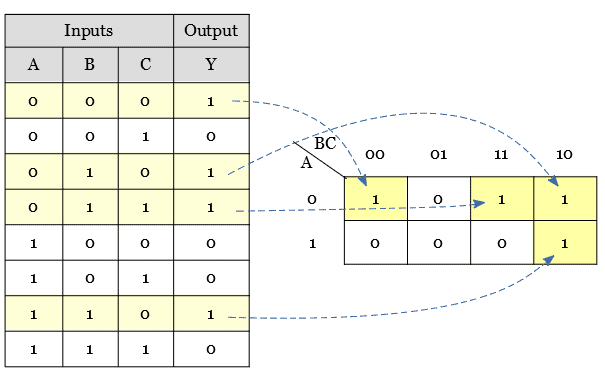
In the above figure, a logic function in a truth table form is considered, which has two inputs(A and B) and one output(Y).
The output produced was true(logic 1) for two input combinations(01, 11) and false(logic 0) for two input combinations(00, 10).
The logic ‘1’ output for an input value AB = ’01’ is plotted to the K-map corresponding to a cell, which has A=’0′, B=’1′ in the label.
The logic ‘1’ output for an input value AB = ’11’ i plotted to the K-map corresponding to a cell, which has A=’1′, B=’1′ in the label.
The logic ‘0’ output for an input value AB = ’00’ is plotted to the K-map corresponding to a cell, which has A=’0′, B=’0′ in the label.
The logic ‘0’ output for an input value AB = ’10’ is plotted to the K-map corresponding to a cell, which has A=’1′, B=’0′ in the label.
In a similar way, a logic function with three inputs and one output can be plotted in an 8-cell K-map and a logic function with four inputs ad one output can be plotted in a 16- cell K-map. For your understanding purpose, the plotting of 8 cells K-map is shown below.
Plotting SOP expression in a K-map
A Boolean SOP expression can also be plotted in a K-map by simply placing a logic 1 in the cell corresponding to a minterm of that expression. The remaining cells are filled with logic 0. Let us look at some examples.
Example Problem 1
Let us plot a Boolean equation Y = A’B’C + ABC’ + A’BC’ + AB’C in a K-map.
The given expression has three variables A, B, and C. Hence 23 = 8 cell K-map is used for plotting the boolean equations.
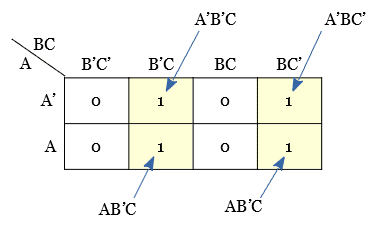
As you see, the above plotting is done by labeling the K-map with the variable name(A, B, and C) and its complement.
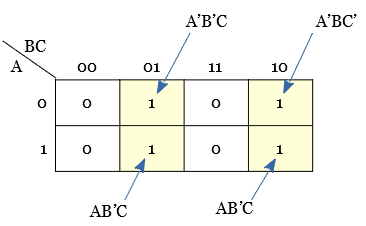
This plotting can be done by replacing the variable and its complement with logic 0 and 1 as shown below.
Example Problem 2
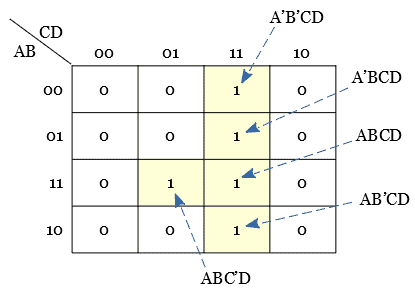
Plot a Boolean expression Y = A’B’CD + A’BCD + AB’CD + ABC’D + ABCD in a Karnaugh map.
The given expression has four variables A, B, C, and D. Hence 24 = 16 cell K-map is used for plotting the expression.
Plotting POS expression in a K-map
A Boolean POS expression can also be plotted in a K-map by simply placing a logic 0 in the cell corresponding to a Maxterm of that expression. The remaining cells are filled with logic 1. Let us look at some examples.
Example Problem 3
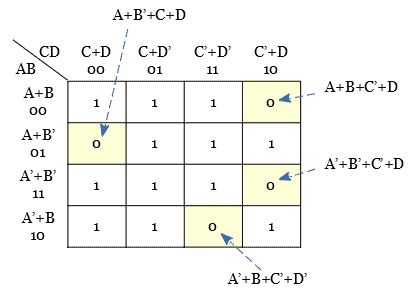
Plot the Boolean function Y = (A+B’+C+D) (A+B+C’+D) (A’+B’+C’+D) (A’+B+C’+D’) in a Karnaugh map.
The given expression has four variables A, B, C, and D. Hence 24 = 16 cell K-map is used for plotting the POS expression.
Grouping cells in Karnaugh map
After plotting the terms in the K-map, we have to simplify it to get a minimal boolean expression. From the simplified expression, a logical diagram can be drawn. For simplification, we go for the grouping of adjacent cells.
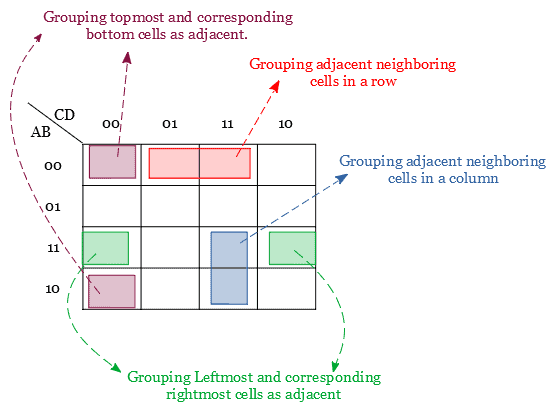
Grouping is nothing but combining the neighbor cells that have common boolean variables to get a simplified expression. Two cells are said to be adjacent if there is only one difference between the coordinates of the two cells.
The adjacent cells can be either neighboring cells in a row or neighboring cells in a column. Also, the leftmost columns can be grouped with the rightmost column and the topmost row with the bottommost row, which is depicted as follows.
Illegal Grouping of cells
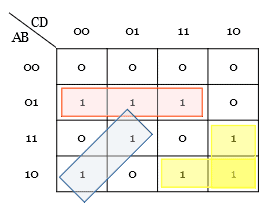
The cells in the K-map cannot be grouped in some ways, which is said to be an illegal grouping. The following image shows the different illegal groupings of cells.
Now, let us discuss the various grouping rules.
Grouping two adjacent cells (Pair)
Look at the following example. As you see, the Karnaugh map contains 3 pairs of 1s, which are vertically adjacent and horizontally adjacent to each other.
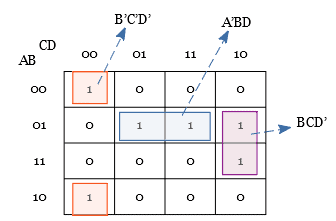
The two adjacent 1s are located at the cells with the terms A’B’C’D’ and AB’C’D’, A’BC’D and A’BCD, A’BCD’ and ABCD’. The three individual pairs of cells can be combined.
In the first pair(A’B’C’D’ and AB’C’D’), in which the input variable A appears in normal and its complement form, whereas B’C’D’ remains unchanged.
Whereas in the second pair(A’BC’D and A’BCD), in which the variable C appears in normal and its complement form, A’BD remains unchanged.
In the third pair(A’BCD’ and ABCD’), in which variable A appears in normal and its complement form, whereas BCD’ remains unchanged.
Thus by combining the three pairs of cells, we get B’C’D’ + A’BD + BCD’ as result. Thus by grouping the adjacent cells, a simplified expression can be obtained.
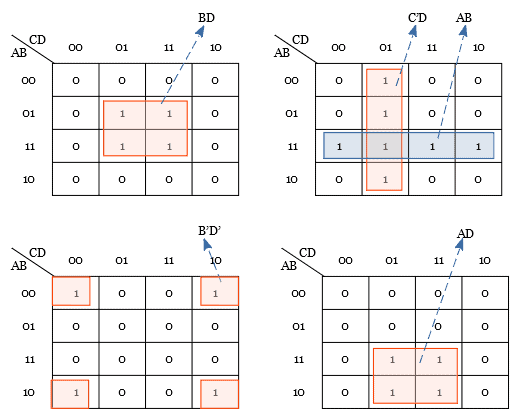
Grouping Four adjacent cells (Quad)
Four neighboring cells can be grouped, which is called quad grouping. Grouping four cells can be done in different ways. Look at some of the examples below.
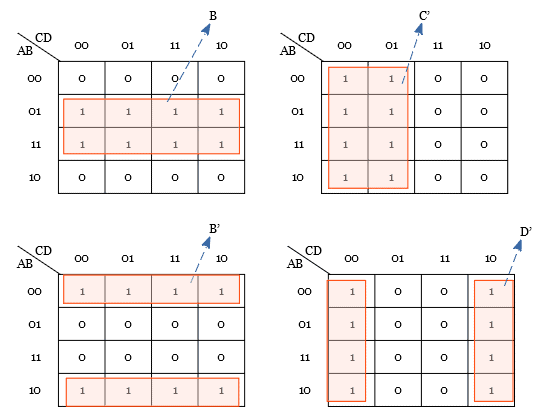
Grouping Eight adjacent cells (Octet)
Eight neighboring cells can be grouped, which is called octet grouping. The octet grouping gives a simplified boolean equation. Grouping eight cells can be done in different ways. Look at some of the examples below.
Essential Prime implicants of K-map
The karnaugh map can be plotted for the given Boolean expressions. This expression may be the sum of product form or the Product of sum form.
The terms in the expression, either minterm or maxterm is called the implicants as they imply the function.
All the possible groups formed using the Karnaugh map are called prime implicants. Look at the below K-map, in which there are 3 groups or 3 prime implicants, marked as 1, 2, and 3.
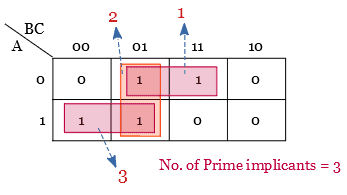
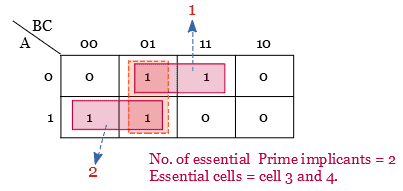
In the above K map, two cells(cells 3 and 4) appear in only one prime implicant group and two cells(cells 1 and 5) appear in more than one prime implicant group.
The cells which appear in only one prime implicant group are called essential cells. The corresponding prime implicants are called essential prime implicants.


Related Posts