How do you convert phasor to complex form?

Mathematical representation of phasor in Complex form

The complex form of representing a phasor is used to solve complex sinusoidal equations. DC analysis requires simple mathematics to solve its equations. Since an AC waveform has magnitude and direction, it needs a complex number to solve AC sinusoidal equations.

A phasor is a rotating vector quantity, that can be represented mathematically in four ways: Rectangular form, trigonometric form, exponential form and Polar form. Before going into the section, let us take a look at the complex numbers.

What is a complex number?

Complex Number was introduced to solve the complex equations, which have both magnitude and direction. A complex number consists of two parts: Real number and Imaginary number.

The real number in the phasor complex number denotes the magnitude of the AC signal. It represents the length of the vector.

The Imaginary number denotes the phase angle of the AC sinusoidal waveform. In order to distinguish the real number from the complex number, the letter ‘j’ is used with an imaginary number. The phasor always rotates in X and Y coordinates when the magnitude and phase angle change.

Rectangular form

In rectangular form, the phasor quantities are algebraically expressed in terms of rectangular components. It is also called a Cartesian form of representation. In this form, a phasor can be divided into two components, namely a horizontal component and a vertical component.

For example, let us consider the phasor E, as shown in the below phasor diagram. From the endpoint of the phasor, draw a horizontal line and vertical line towards the X-axis and Y-axis respectively. Now, the phasor E is said to have horizontal component ‘a’ and vertical component ‘b’.

Thus in rectangular form, the phasor can be mathematically expressed as

$\boxed{ E = a + jb}$

Here ‘j’ is a complex operator, which indicates that the component ‘b’ is perpendicular to component ‘a’. In this way of writing an expression is said to be a complex form of the phasor.

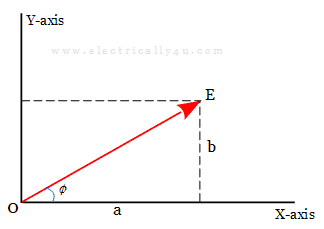
Mathematically, the component ‘a’ along the horizontal axis is called a real number and component ‘b’ along the vertical axis is called an imaginary number. In electrical engineering, it is called active and reactive components respectively.

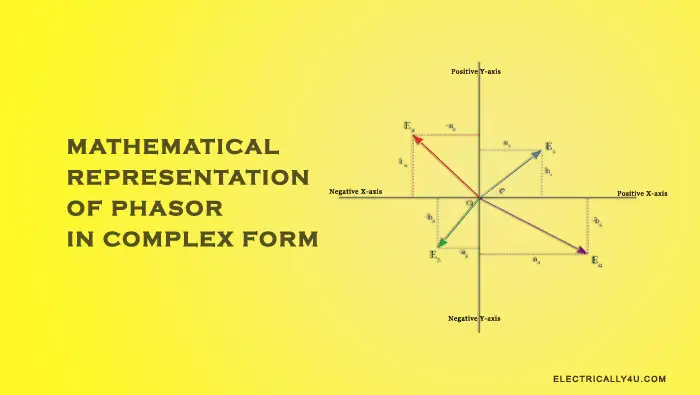
Both the real and imaginary parts of a complex number can be either positive or negative. Hence both the real and imaginary axis extended in respective positive and negative directions. It results in a complex plane with four quadrants called an Argand Diagram, as shown below.

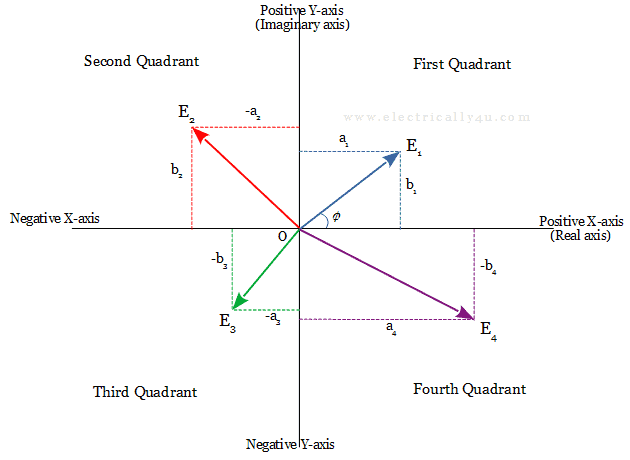
In the Argand diagram, there are four phasors each in four quadrants of the complex plane. In rectangular form, the four phasors are represented as,

$OE_1 = a_1 + jb_1, OE_2 = -a_2 + jb_2, OE_3 = -a_3 - jb_3, OE_4 = a_4 - jb_4$

Significance of j operator

In general, an operator such as +, -, *, / performs some operations on the numbers. Similarly, j is a complex operator, which indicates the location of the phasor that is rotating in anticlockwise direction. The value for ‘j‘ is given by j = √-1 or j² = -1 .

Let E be the phasor in the horizontal X-axis, which rotates in the anticlockwise direction. When the j operator is joined with the phasor E, it becomes jE and is displaced through 90⁰. When the j operator is again multiplied with jE, the phasor becomes j²E = -E. Now the phasor -E is rotated through an angle 180⁰.

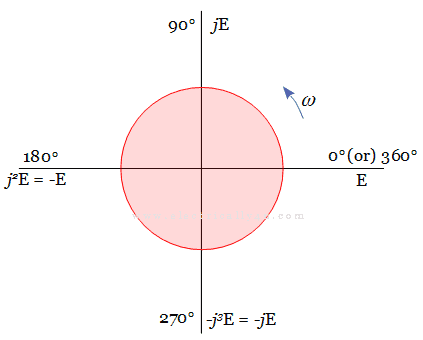
Further application of j operator on -E, it becomes –jE and this phasor is displaced by 270⁰. It is directly opposite to the phasor jE. When the j operator is again applied to the phasor –jE, it becomes –j²E = E. Now the phasor completes 360⁰ rotation, returning back to its original position.

The significance of j operator can be summarized as below,

90⁰ rotation; $j = \sqrt{-1} = +j$

180⁰ rotation; $j^2 = {( \sqrt{-1} )}^2 = -1$

270⁰ rotation; $j^3 = {( \sqrt{-1} )}^3 = -j$

360⁰ rotation; $j^4 = {( \sqrt{-1} )}^4 = +1$

Trigonometric form

Let us consider a phasor OB having the magnitude E and it is displaced by an angle Φ with respect to X-axis. Draw a vertical line from B towards the horizontal axis. Now OAB is a right-angled triangle.

By applying trigonometry to the triangle, we obtain,

$cos \phi = \frac{OA}{OB} = \frac{OA}{E} => OA = E cos\phi$

$sin\phi = \frac{AB}{OB} = \frac{AB}{E} => AB = E sin\phi$

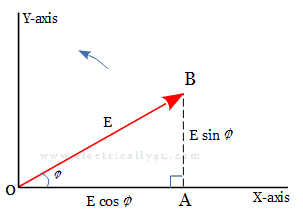
It is observed that, the horizontal component of E is E cosϕ and its vertical component is $ E sinϕ. Thus in trigonometric form, we can represent the phasor as,

$\boxed{ E = E cos \phi + j E sin \phi }$

This is equivalent to the rectangular form E = a + jb,

where a = E cosϕ and b = E sinϕ.

Exponential form

Euler’s formula gives the relationship between the exponential and trigonometry functions. It is given by,

$e^{j\phi} = cos \phi + j sin \phi$

Also, in Maclaurin series, the functions sinϕ, cosϕ and e^jϕ are expanded as,

$cos \phi = 1 - \frac{1}{2!} \phi^2 + \frac{1}{4!} \phi^4 - \frac{1}{6!} \phi^6 + ... --->(1)$

$sin \phi= \phi - \frac{1}{3!} \phi^3 +\frac{1}{5!} \phi^5 - \frac{1}{7!} \phi^7 + ... --->(2)$

$e^{j\phi} = 1 + j \phi + \frac{1}{2!} {j \phi}^2 + \frac{1}{3!} {j \phi}^3 + \frac{1}{4!} {j \phi}^4 + \frac{1}{5!} {j \phi}^5 + \frac{1}{6!} {j \phi}^6 + \frac{1}{7!} {j \phi}^7 + ...$

As we know, j² = -1, j³ = -j, j⁴ = +1, j⁵ = +j, j⁶ = -1, j⁷ = -j…, the above expression for e^jϕ is re-written as,

$e^{j\phi} = 1 + j \phi - \frac{1}{2!} \phi^2 - \frac{j}{3!} \phi^3 + \frac{1}{4!} \phi^4 + \frac{j}{5!} \phi^5 - \frac{1}{6!} \phi^6 - \frac{j}{7!} \phi^7 ...$

$e^{j\phi} = \left(1 - \frac{1}{2!} \phi^2 + \frac{1}{4!} \phi^4 - \frac{1}{6!} \phi^6 + ... \right) + j \left( \phi - \frac{1}{3!} \phi^3 +\frac{1}{5!} \phi^5 - \frac{1}{7!} \phi^7 + ... \right )$

Using equations (1) and (2), the above expression becomes,

$e^{j\phi} = cos \phi + j sin \phi$

Thus the trigonometric form of a phasor E = E(cosϕ + j sinϕ) can be written in exponential form as,

$\boxed{ E = E e^{j\phi} }$

In the exponential form of a phasor, E represents the magnitude and ϕ represents the phase angle with respect to the reference axis.

Polar form

In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction.

In complex polar form, the phasor is represented with its magnitude and phase angle as,

$\boxed{ E = E \angle \pm \phi }$

Here E is the magnitude of the phasor, ϕ is the angle of the phasor with respect to X-axis.

Let us draw this phasor having the magnitude E, leading by angle ϕ with respect to the horizontal axis. If the arrowhead of E is joined with a vertical line towards the horizontal axis, we get a right-angled triangle.

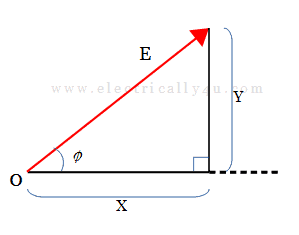
By using the Pythagoras theorem, it is possible to determine the magnitude and angle of the complex number.

The Pythagoras theorem relates the sides of a right angled triangle in a simple way

${E}^2 = x^2 + y^2$

$\boxed{ E = \sqrt{x^2 + y^2} }$

By applying trigonometry, we can also write,

$cos \phi = \frac{x}{E} => x = E cos\phi .........(1)$

$sin\phi = \frac{y}{E} => y = E sin\phi ..........(2)$

Dividing the equation(2) by eqution(1), we get,

$\frac{sin \phi}{cos \phi} = \frac{y}{x} => tan \phi = \frac{y}{x}$

$\boxed{\phi = tan^{-1} \frac{y}{x}}$

Summarizing the different forms to represent the phasor quantities,

Rectangular form: E = a ± jb

Trigonometric form : E = E (cosϕ ± j sinϕ)

Exponential form: E = E e^±jϕ

Polar form: E = E ∠ ± ϕ

It is possible to convert one form to another when the coordinates of a system are known. Use the Rectangular and Polar Conversion tool to convert from polar coordinates to rectangular coordinates(or cartesian coordinates) and vice versa

Complex Arithmetic operation of phasor

Two or more phasor quantities can be added, subtracted, multiplied, divided using the rectangular, trigonometric, exponential and polar forms. Let us learn, how each operation are performed.

Phasor Addition

The rectangular form is sufficient to perform the addition and subtraction operation of phasor quantities.

Let us consider the two voltage waveforms, 15 volts and 23 volts with same frequency and are in- phase with ech other. In this case, to find the sum of the two voltages, just add them to get 38 volts.

If the two voltages have different phases, which are out of phase. Then you cannot add them directly to find the overall voltage. This is because, the two wave forms having different directions.

Consider the complex number of two phasors, A = a₁ + jb₁ and A = a₂ + jb₂ for which the addition operation is to be performed.

For addition,

$E = A + B = (a_1 + j b_1 ) + (a_2 + j b_2) = (a_1 + a_2) +j(b_1 + b_2)$

The magnitude of resultant phasor is determined as,

$E = \sqrt{(a_1+a_2)^2 + (b_1 +b_2)^2}$

Phase angle with respect to X-axis is,

$\phi = tan^{-1} \left(\frac{b_1 +b_2}{a_1 + a_2} \right)$

Phasor Subtraction

For subtraction,

$E = A - B = (a_1 + j b_1 ) - (a_2 + j b_2) = (a_1 - a_2) +j(b_1 - b_2)$

Its magnitude is obtained as,

$E = \sqrt{(a_1-a_2)^2 + (b_1 -b_2)^2}$

Phase angle with respect to X-axis is,

$\phi = tan^{-1} \left(\frac{b_1 -b_2}{a_1 - a_2}\right)$

Phasor Multiplication

Performing the phasor multiplication and phasor division by using the rectangular form is complex. But by using polar form or exponential form, the operation will be very simple.

Let us consider the two phasors, A = a₁ + jb₁ and A = a₂ + jb₂ .

In polar form of representation,

$A = a_1 + j b_1 = A \angle \phi_1$

$B = a_2 + j b_2 = B \angle \phi_2$

The resultant phasor is given by,

$A*B = A \angle \phi_1 + B \angle \phi_2 = AB \angle{(\phi_1 +\phi_2)}$

Hence, it is observed that the product of any two phasors is given by another resultant phasor, whose magnitude is given by A*B and the phase angle is equal to the sum of angles of A and B.

Phasor Division

Similarly for division,

$\frac{A}{B} = \frac{A \angle \phi_1}{B \angle \phi_2} = \frac{A}{B} \angle{(\phi_1 -\phi_2)}$

Here, it is observed that the quotient of any two phasors results in another phasor, whose magnitude is given by (A/B) and the phase angle is equal to the angle of A minus the angle of B.

Conjugate of a complex number

The Conjugate of a complex number (or simply Complex Conjugate) is obtained just by reversing the algebraic sign of the imaginary number. In this complex conjugate, the algebraic sign of the real number remains the same.

Let z be the complex number and its conjugate is represented as z bar(z’). For example, the conjugate of the complex number z = 5 + 6j is z’ = 5 – 6j. Similarly, the complex conjugate of z = 5 – 6j is z’ = 5 + 6j.

On the Argand diagram, a complex conjugate has the same horizontal position on the real axis as the original complex number, but opposite vertical positions. Thus, complex conjugates can be thought of as a reflection of a complex number. The following example shows a complex number, 6 + j4 and its conjugate in the complex plane.

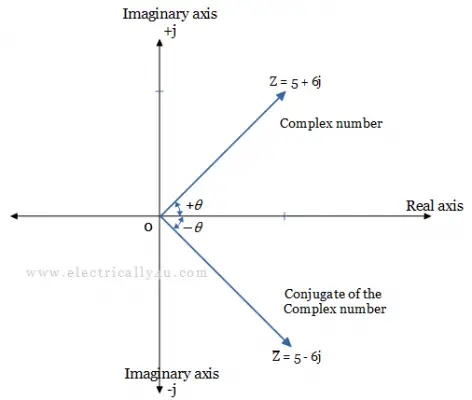
What happens when a complex number and its conjugate are separately added and subtracted?

If you add the complex number 5 + 6j and its conjuagte 5 – 6j, you get (5 + 6j) + (5 – 6j) = 10.

As you could see, the obtained result is only a real number or active component.

When they are subtracted, you will get (5 + 6j) – (5 – 6j) = 12j.

Thus for subtraction, the obtained result will be the imaginary number only or reactive component.

The conjugate of a complex number is important to determine the apparent power of an AC circuit using the rectangular form.

In DC circuit, the power is given by P = VI, whereas in an AC circuit, the total power is given by S = P + jQ, which is called complex power. P denotes the real power in the circuit and Q denotes the reactive power (power flowing back and forth). The magnitude S denotes the apparent power.

FAQs

A phasor has both magnitude and direction, which rotates in the anti-clockwise direction. The phasor is converted into a complex form by drawing the magnitude along the horizontal axis and the direction along the vertical axis.

Mathematical representation of phasor in Complex form

What is a complex number?