Nodal Analysis

ByAbragam Siyon Sing Updated on
Nodal Analysis

Nodal analysis is a method to analyze a complex circuit using Kirchoff’s current law to find the voltages in the electric circuit. As the name suggests, the analysis is carried out with reference to each node in the circuit. Nodal Analysis is just the complement of the mesh or loop analysis.

In this analysis, the voltage drop is measured with the respect to two nodes. One is the main node and the other is the reference node. Generally, the grounded node is considered as the reference node.

Steps to solve nodal analysis method

  1. The nodal analysis makes the analysis simpler only if the circuit has only current sources. If any voltage source is present in the circuit, prior to the nodal analysis, the voltage source has to be converted into the current source by the source transformation method.

Let us consider a simple circuit, as shown below

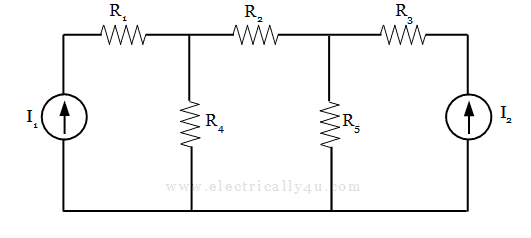
Nodal Analysis_1
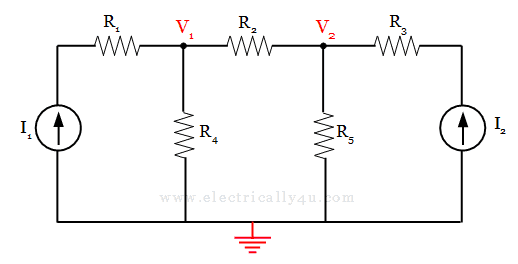
  1. Identify all the principal nodes in the circuit and choose a reference node. All the nodes except the reference node are numbered and the corresponding voltages are designated as V1, V2,… The reference node can be grounded.

In the considered circuit, there are two principal nodes and are designated as V1 and V2. The bottom node is considered a reference node and is grounded for identification.

Nodal Analysis_2
  1. Assign the currents to each branch. Express the branch currents in terms of node voltages by using Ohm’s Law.
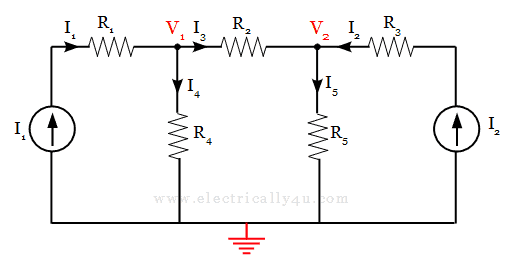
Nodal Analysis_3

The branch currents can be expressed as

    \[ I_3 = \frac{V_1 - V_2}{R_2}, I_4 = \frac{V_1 - 0}{R_4}, I_5 = \frac{I_5 - 0}{R_5} \]

  1. Apply Kirchoff’s Current Law(KCL) for all the nodes(except reference node) and write the nodal equations.
  2. Solve the KCL equations to get the node voltages.

Solved Problem 1

Determine the current through each resistor in the given circuit using nodal analysis.

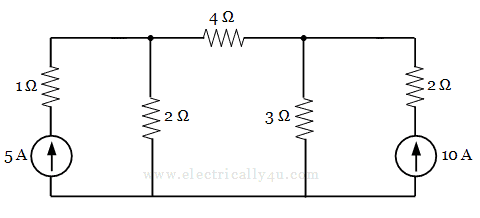
In this circuit, there are two nodes, which are designated as V1 and V2. The bottom nodes are together considered as a reference node(grounded). The currents are assigned in each branch and the circuit is redrawn as below.

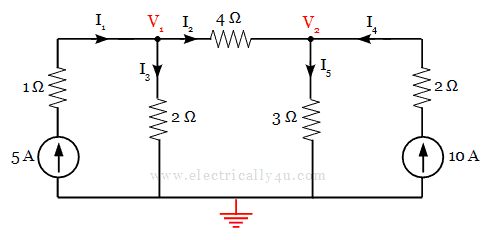
Apply Kirchoff’s Current Law at node 1,

    \[ I_1 = I_2 + I_3 \]

    \[ 5 = \frac{V_1 - V_2}{4} + \frac{V_1}{2} \]

    \[0.25 V_1 - 0.25V_2 + 0.5V_1 = 5\]

    \[ 0.75V_1 - 0.25V_2 = 5 --->(1)\]

Apply KCL at node 2,

    \[I_4 + I_2 = I_5 \]

    \[10 + \frac{V_1 - V_2}{4} = \frac{V_2}{3} \]

    \[ 0.25V_1 - 0.25V_2 - 0.33V_2 = -10 \]

    \[ 0.25V_1 - 0.58V_2 = -10 --->(2)\]

The above two equations are written in matrix form, as shown below,

    \[ \begin{bmatrix} 0.75 & -0.25 \\ 0.25 & -0.58 \end{bmatrix} \begin{bmatrix} V_1 \\ V_2 \end{bmatrix} = \begin{bmatrix} 5 \\ -10 \end{bmatrix} \]

Applying Cramer’s rule, we get

    \[ \Delta = \begin{vmatrix} 0.75 & -0.25 \\ 0.25 & -0.58 \end{vmatrix} = -0.435 + 0.0625 = -0.373 \]

    \[ \Delta_1 = \begin{vmatrix} 5 & -0.25 \\ -10 & -0.58 \end{vmatrix} = -2.9 - 2.5 = -5.4 \]

    \[ \Delta_2 = \begin{vmatrix} 0.75 & 5 \\ 0.25 & -10 \end{vmatrix} = -7.5 - 1.25 = -8.75 \]

Now, the node voltages is determined

    \[V_1 = \frac{\Delta_1}{\Delta} = \frac{-5.4}{-0.373} = 14.47 V\]

    \[V_2 = \frac{\Delta_2}{\Delta} = \frac{-8.75}{-0.373} = 23.46 V\]

The branch currents are determined as follows

    \[I_1 = 5 A\]

    \[I_2 = \frac{V_1 - V_2}{4} = \frac{14.47 - 23.46}{4} = -2.24 A \]

    \[I_3 = \frac{V_1}{2} = \frac{14.47}{2} = 7.23 A\]

    \[ I_4 = 10 A\]

    \[ I_5 = \frac{V_2}{3} = \frac{23.46}{3} = 7.82 A \]

Solved Problem 2

Find the different nodal voltages in the given circuit.

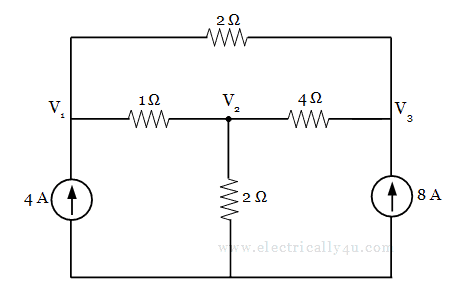
In this circuit, there are three given nodes, which are designated as V1, V2 and V3. For these three nodes, we have to write the current equations by applying KCL. Before that, let us assign the current in each branches and redraw the circuit.

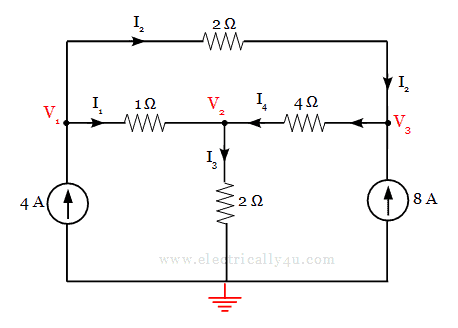
Apply Kirchoff’s Current Law at node 1,

    \[4 = I_1 + I_2\]

    \[ 4 = \frac{V_1 - V_2}{1} + \frac{V_1 - V_3}{2}\]

    \[1.5V_1 - V_2 - 0.5V_3 = 4 --->(1) \]

Apply KCL at node 2,

    \[I_1 + I_4 = I_3\]

    \[\frac{V_1 - V_2}{1} + \frac{V_3 - V_2}{4} = \frac{V_2}{2}\]

    \[V_1 - 1.25V_2 - 0.25V_3 = 0 --->(2)\]

Apply KCL at node 3,

    \[8 + I_2 = I_4\]

    \[8 + \frac{V_1 - V_3}{2} = \frac{V_3 - V_2}{4}\]

    \[0.5V_1 + 0.25V_2 - 0.75V_3 = -8 --->(3)\]

The above three equations are written in matrix form, as shown below,

    \[ \begin{bmatrix} 1.5 & -1 & -0.5 \\ 1 & -1.25 & -0.25 \\ 0.5 & 0.25 & -0.75 \end{bmatrix} \begin{bmatrix} V_1 \\ V_2 \\ V_3 \end{bmatrix} = \begin{bmatrix} 4 \\ 0 \\ -8 \end{bmatrix} \]

Applying Cramer’s rule, we get

    \[ \Delta = \begin{vmatrix} 1.5 & -1 & -0.5 \\ 1 & -1.25 & -0.25 \\ 0.5 & 0.25 & -0.75 \end{vmatrix}\]

    \[\Delta = 1.5(0.94+0.063)+1(-0.75+0.125)-0.5(0.25+0.625) = 0.442 \]

    \[ \Delta_1 = \begin{vmatrix} 4 & -1 & -0.5 \\ 0 & -1.25 & -0.25 \\ -8 & 0.25 & -0.75 \end{vmatrix} = 4(0.94+0.063)+1(0-2)-0.5(0-10)=7.012 \]

    \[ \Delta_2 = \begin{vmatrix} 1.5 & 4 & -0.5 \\ 1 & 0 & -0.25 \\ 0.5 & -8 & -0.75 \end{vmatrix} = 1.5(0-2)-4(-0.75+0.125)-0.5(-8+0)=3.5 \]

    \[ \Delta_3 = \begin{vmatrix} 1.5 & -1 & 4 \\ 1 & -1.25 & 0 \\ 0.5 & 0.25 & -8 \end{vmatrix} = 1.5(10-0)+1(-8-0)+4(0.25+0.625)=10.5 \]

Now, the node voltages are determined

    \[V_1 = \frac{\Delta_1}{\Delta} = \frac{7.012}{0.442} = 15.86 V\]

    \[V_2 = \frac{\Delta_2}{\Delta} = \frac{3.5}{0.442} = 7.92 V\]

    \[V_3 = \frac{\Delta_3}{\Delta} = \frac{10.5}{0.442} = 23.76 V\]

1 Shares

An Assistant Professor in the Department of Electrical and Electronics Engineering, Certified Energy Manager, Photoshop designer, a blogger and Founder of Electrically4u.

Related Posts

Leave a Reply

Your email address will not be published. Required fields are marked *

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

One Comment