Universal Logic gates

Universal logic gates are used to build all other logic functions. NAND gate and NOR gate are known as universal logic gates. With these two gates, other logic functions like AND, OR, NOT, NOR, EX-OR or Ex-NOR can be implemented.
In a digital circuit comprising of different basic gates, some ICs remain unused during its operation and so the utility factor is very low. The utility factor can be improved when only one logic gate is used to implement the logic function. Let us discuss the two universal logic gates, NAND gate and NOR gate in detail.
NAND gate – A Universal Logic gate
The NAND gate is used to generate all the logical functions like AND, OR, NOT and NOR. Do read about the NAND gate here.
Let us see how AND gate is realized.
Realization of NOT function
The truth table for NOT gate is
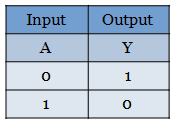
Lets see how the truth table for NOT gate be implemented with only NAND gate.
The boolean expression for NOT gate is
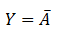
The above expression is realized by replacing the NOT gate with a single input NAND gate.
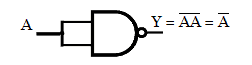
The truth table for realizing the NOT gate from the NAND gate is shown below.
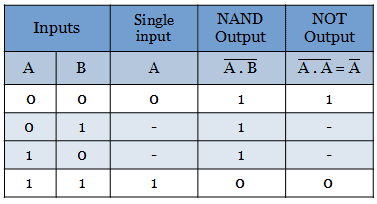
Realization of AND function
The truth table for AND gate is
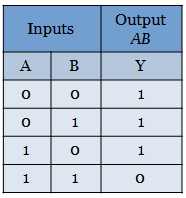
The above truth table for AND gate can be implemented with only NAND gate. The boolean expression for AND gate is Y = AB.
This is obtained by inserting a NOT gate at the output side of NAND gate. So it becomes double inversion. The double inversion cancels each other to become AB, as shown below.
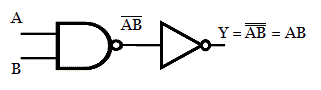
The NOT gate in the above realization is replaced with single input NAND gate to get the circuit with desired output function.
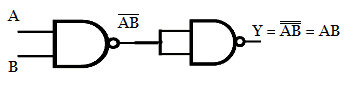
The truth table for realizing the AND gate from the NAND gate is shown below.
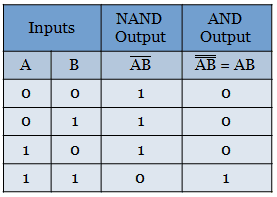
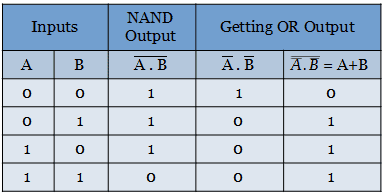
Realization of OR function
The truth table for OR gate is
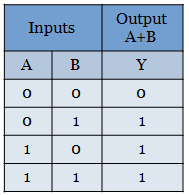
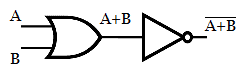
Lets see how the truth table for OR gate be implemented with only NAND gate. The boolean expression for OR gate is Y = A+B.
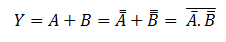
The above relation is obtained by applying the Postulates and theorems of Boolean Algebra. The above expression is realized by inserting a NOT gate at the two input side of NAND gate.
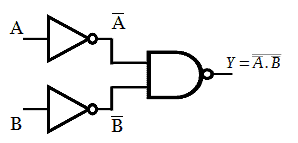
The NOT gate in the above realization is replaced with single input NAND gate to get the circuit with desired output function.
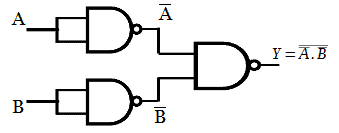
The truth table for realizing the OR gate from the NAND gate is shown below.
Implementation using NAND gates
Any logic function can be implemented using NAND gates by following the below steps.
- For the given logic function, draw the logic circuit using the basic gates(AND, OR, NOT gates)
- Add bubbles at the input side of OR gate and at the output side of AND gate.
- Place a NOT gate wherever bubbles are added in the previous step.
- Eliminate any double inversion.
- Replace all the gates with a NAND gate.
Implementation of NOR function using NAND gates.
The boolean expression for NOR gate is
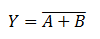
Step 1: Draw the logic circuit for the above expression using AND, OR, NOT gate.
Step 2: Add bubbles at the input of OR gate.
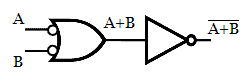
Step 3: Place NOT gate at the bubbles.
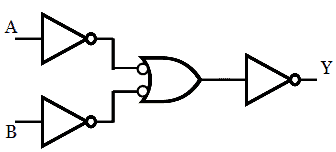
Step 4: Eliminate double inversion. No double inversion is here.
Step 5: Replacing all the gates with a NAND gate, we get the desired logic circuit.
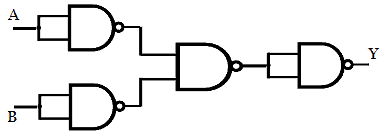
Implementation of Ex-OR function using NAND gates.
The boolean expression for Ex-OR gate is
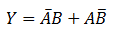
Step 1: Draw the logic circuit for the above expression using AND, OR, NOT gate.
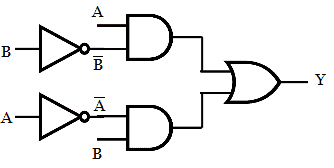
Step 2: Add bubbles at the input of OR gate and at the output of AND gate.
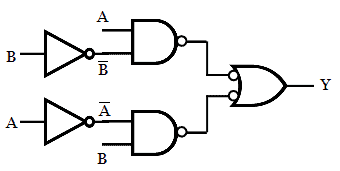
Step 3: Place a NOT gate wherever bubbles are added.
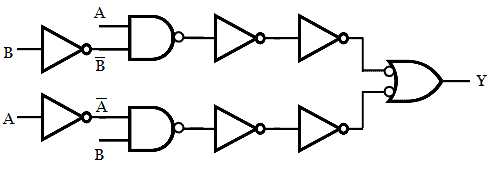
Step 4: Eliminate double inversion.
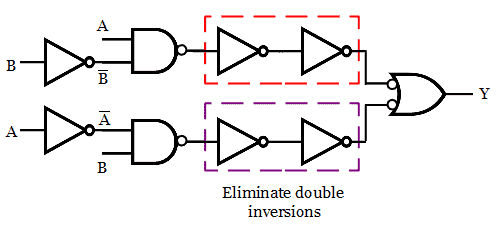
Eliminating the double inversions, we get the below circuit.
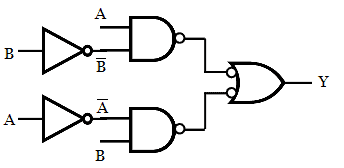
Step 5: Replacing all the gates with a NAND gate, we get the desired logic circuit.
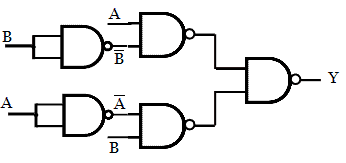
Implementation of Ex-NOR function using NAND gates.
The boolean expression for Ex-NOR gate is
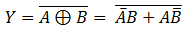
The Ex-NOR gate is the inversion of Ex-OR gate, so from the previous implementation of Ex-OR function using NAND gate, just add a NOT gate to invert the output in order to get the desired output circuit. Since we have realized the NOT gate with NAND gate, instead of NOT gate, place a single input NAND gate.
NOR gate – A Universal Logic gate
NOR gate is also called as Universal gate. Similar to the NAND gate, it is also used to generate the logical functions of AND gate, OR gate, NOT gate and NAND gate. While realizing all the logic functions, only NOR gates are used. Do read about the NOR gate here.
Lets see how the basic logical function is realized using only NOR gates.
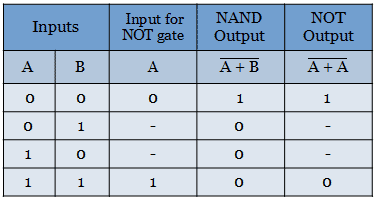
Realization of NOT function
The NOT function can be implemented by using the NOR gate by replacing the NOT gate with a single input NOR gate, as shown below.
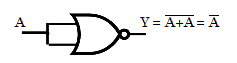
The truth table for realizing the NOT gate from the NOR gate is shown below.
Realization of AND function
The boolean expression for AND gate is Y = (A . B). For realization using NOR gate, the boolean expression can be obtained as
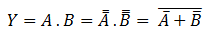
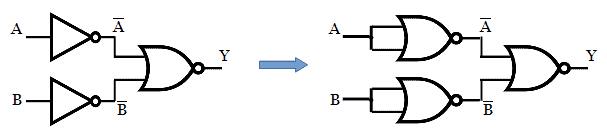
The above expression is implemented using NOR gate as
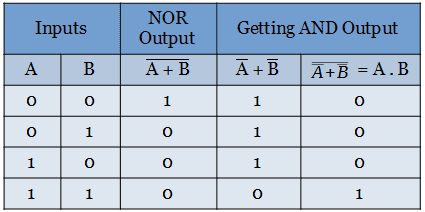
The truth table for realizing the AND gate from the NOR gate is shown below.
Realization of OR function
The boolean expression for AND gate is Y = A+B. This is obtained by inserting a NOT gate at the output side of NOR gate. So it becomes double inversion. The double inversion cancels each other to become A+B, as shown below.

The truth table for realizing the OR gate from the NOR gate is shown below.
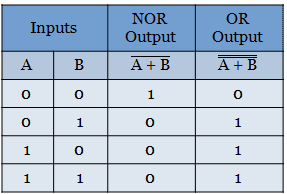
Implementation using NOR gates
Any logic function can be implemented using NOR gates by following the below steps.
- For the given logic function, draw the logic circuit using the basic gates(AND, OR, NOT gates)
- Add bubbles at the input side of AND gate and at the output side of OR gate.
- Place a NOT gate wherever bubbles are added in the previous step.
- Eliminate any double inversion.
- Replace all the gates with a NOR gate.
Implementation of NAND function using NOR gates.
The boolean expression for NAND gate is
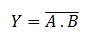
Step 1: Draw the logic circuit for the above expression using AND, OR, NOT gate.
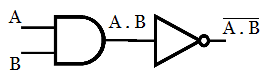
Step 2: Add bubbles at the input of AND gate.
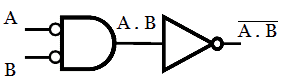
Step 3: Place NOT gate at the place where bubbles are added.
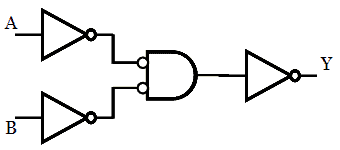
Step 4: Eliminate double inversion. No double inversion is here.
Step 5: Replacing all the gates with a NOR gate, we get the desired logic circuit.
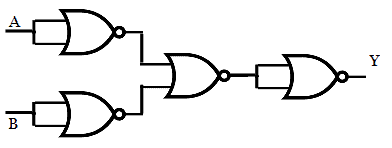
Implementation of Ex-OR function using NOR gates.
The boolean expression for Ex-OR gate is
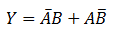
Step 1: Draw the logic circuit for the above expression using AND, OR, NOT gate.
Step 2: Add bubbles at the input of AND gate and at the output of OR gate.
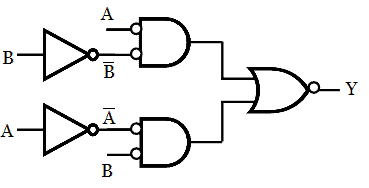
Step 3: Place a NOT gate wherever bubbles are added.
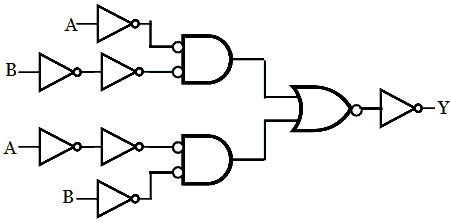
Step 4: Eliminate double inversion.
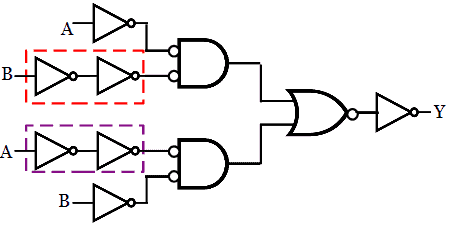
After Eliminating the double inversion in the above circuit,
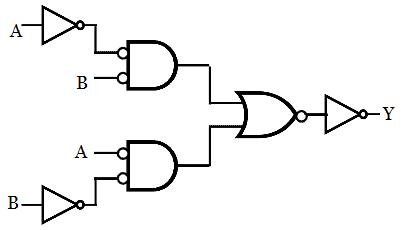
Step 5: Replacing all the gates with a NOR gate, we get the desired logic circuit.
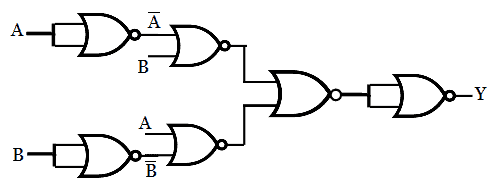
Implementation of Ex-NOR function using NOR gates.
The boolean expression for Ex-NOR gate is
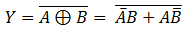
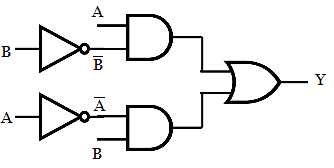
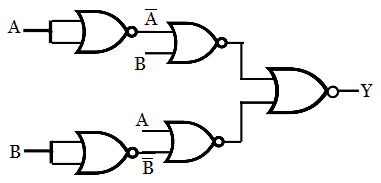
The Ex-NOR gate is the inversion of Ex-OR gate, so from the previous implementation of Ex-OR function using NOR gate, just adding a NOT gate will invert the output. Since there is another NOT gate at the output side, they will be eliminated due to double inversion. Thus the circuit becomes
Any boolean expression(either in SOP form or in POS form) can be implemented using the Universal logic gates, either by using NAND gate or by using NOR gate.

Related Posts