Arithmetic operation of binary numbers

The arithmetic operation of binary numbers include the basic operations like binary addition, binary subtraction, binary multiplication and binary division. Let’s take a look at each of the operation.
Before proceeding, take your time to know about the different number system. Read here.
Binary Addition
The binary addition consists of four possible elementary operations as shown below.
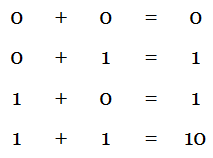
From the above, it is seen that, the first three operations produce a sum whose length is one digit, but for the last operation, the produced sum has two digits.
The higher significant bit of the two digits is called carry and lower significant bit is called as sum. The above discussed operation is called as half addition.
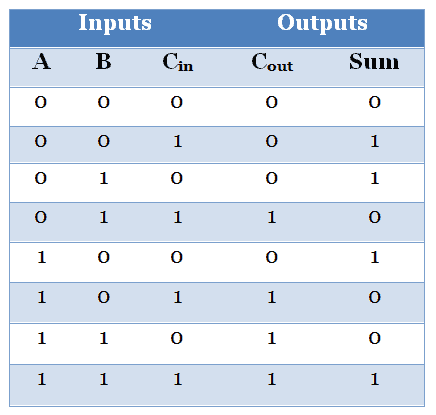
On the other side, if the operation is performed by adding three bits is called full addition. The following table shows the truth table for the operation of full addition.
How to add two binary numbers?
- Add the bits, column-wise starting from LSB with carry if any.
- Place the sum value at the bottom of the same column.
- Place the carry, if any, on the top of the next column from LSB.
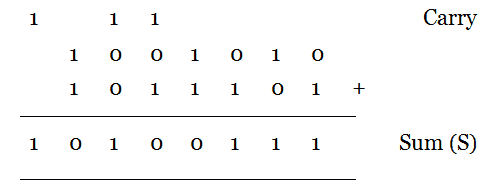
Let us see an example here. Perform binary addition of (1001010)2 and (1011101)2.
Binary Subtraction
The subtraction consists of four possible elementary operations as shown below.
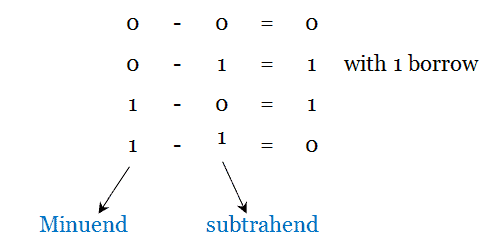
How to subtract two binary numbers?
- Subtract the bits column-wise starting from LSB with borrow if any.
- Place the difference at the bottom of the same column.
- Take the borrow, if required from the next column starting from LSB.
Let us see an example here. Perform binary subtraction of (1101101)2 from (1111011)2.
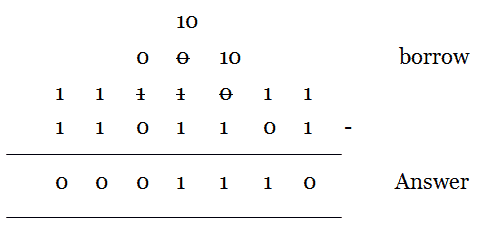
The implementation of this subtraction is difficult for digital computers to perform. So the computer uses complement of numbers to perform the subtraction operation.
Now let us discuss the steps to perform the binary subtraction using 1’s complement and 2’s complement.
How to subtract two binary numbers using 1’s complement?
Before proceeding to the subtraction process using 1’s complement, you have to understand, what exactly is 1’s complement?
1’s Complement
1’s complement of a binary number is obtained by changing all the 1’s to 0’s and 0’s to 1’s.
To make you understand, lets find the 1’s complement of (10101101)2.
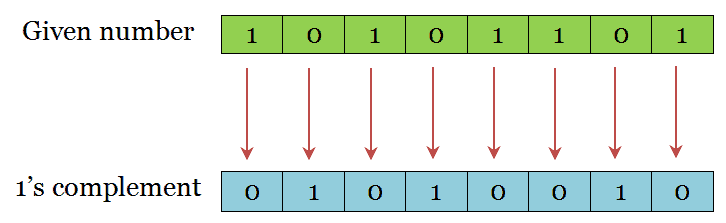
Now, Consider the operation A – B. Read the process to subtract B from A.
- First, Take 1 ‘s complement of B.
- Add A+1’s complement of B.
- If carry is generated, then the result is positive and so add carry to the result to get the final value.
- If carry is not generated, then the result is negative and so write the result in 1’s complement form.
Let us see an example here. Perform binary subtraction of (1101101)2 from (1011011)2 using 1’s complement.

Let’s look at another example. Perform the binary subtraction using 1’s complement of the following: (01111)2 – (11100)2

How to subtract two binary numbers using 2’s complement?
Before proceeding to the subtraction process using 2’s complement, you have to understand, what exactly is 2’s complement?
2’s Complement
2’s complement of a binary number is obtained by adding 1 to the 1’s complement of the given number.
To make you understand, lets find the 2’s complement of (11010010)2.
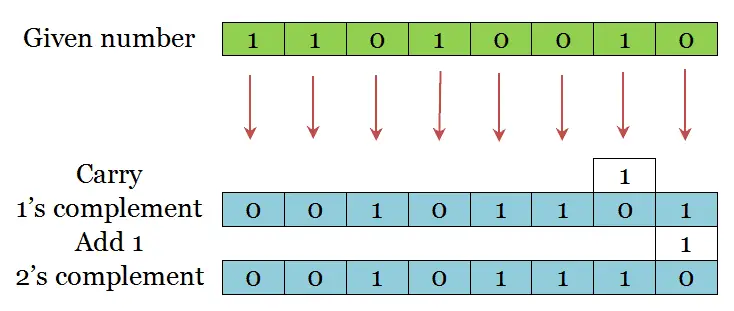
Now, Consider the operation A – B. Read the process to subtract B from A.
- First, Take 2’s complement of B.
- Add A+2’s complement of B.
- If carry is generated, then the result is positive and so ignore the carry to get the final value.
- If carry is not generated, then the result is negative and so write the result in 2’s complement form.
Let us see an example here. Perform binary subtraction of (68)10 from (42)10 using 2’s complement.

Since we have taken 2’s complement of the answer, the obtained result is negative. Thus (0011010)2 = (-26)10.
Let’s solve another example. Perform (11001001)2 – (01011001)2 using 2’s complement.

Binary Multiplication
Binary multiplication is very simple as it is very much similar to the decimal multiplication. It consists of four possible elementary operations as shown below.
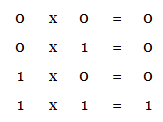
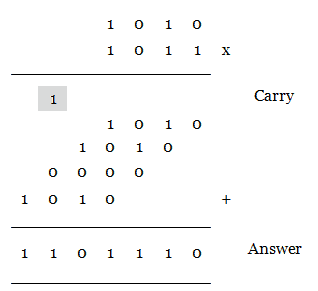
Let us see an example problem. Perform binary multiplication for (1010)2 and (1011)2.
Binary Division
Binary division is also similar to the decimal division, but here division is made between only two numbers 0 and 1. In binary division, division by 0 has no meaning.
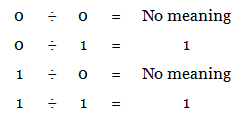
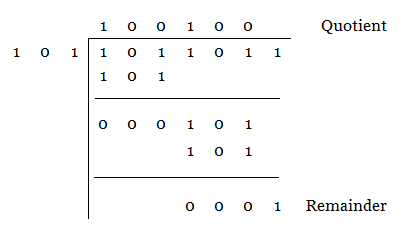
Let us see an example problem. Divide (1011011)2 and (101)2.


Related Posts