Number system conversion

As we are dealing with the electronic system and digital system in our daily life, we should be aware of the different number system conversion. There are different ways to convert one number system to the other. Take a look at how it is computed.

Converting a decimal number to any number system

A decimal number has two parts, integer and fractional part. The integer part is converted by successive division method and the fractional part is converted by successive multiplication method.

In successive division method,

1. Divide the integer part of the given decimal number by desired base number, store the quotient(Q) and the remainder(R).
2. Consider the quotient(Q) as the new decimal number and repeat the step 1 until the quotient(Q) becomes 0.
3. List the remainder in the reverse order to get the desired output.

In successive multiplication method,

1. Multiply the fractional part of the given decimal number by the desired base number to get a decimal number with integer part and fractional part.
2. Store the integer part of the product as Integer value and the factional part as the new fractional part.
3. Repeat the step 1 and 2 until the fractional part of the product becomes 0 or until you obtained the necessary digits.
4. List the carries downwards to get the desired output.

Example 1: Decimal to Binary number conversion

Convert (23.12)₁₀ to a binary number.

Solution.

Integer part conversion is done by successive division method.

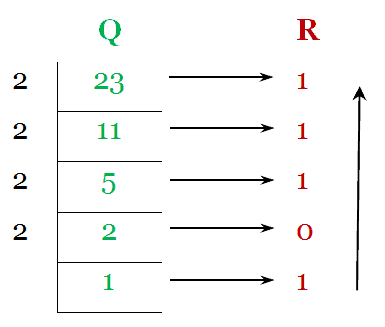
For Integer part, we get, (23)₁₀ = (10111)₂

Fractional part conversion is done by successive multiplication method.

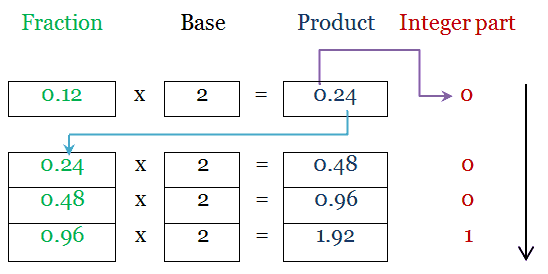
For Fractional part, we get, (0.12)₁₀ = (0.0001)₂

The solution for the given decimal number (23.12)₁₀ = (10111.0001)₂

Example 2: Decimal to Octal number conversion

Convert (263.87)₁₀ to octal number.

Solution.

Integer part conversion is done by successive division method.

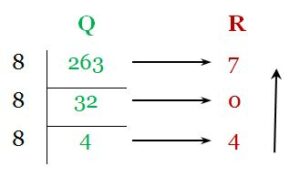
For Integer part, we get, (263)₁₀ = (407)₈

Fractional part conversion is done by successive multiplication method.

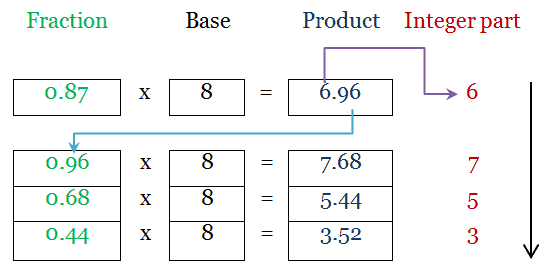
For Fractional part, we get, (0.87)₁₀ = (0.6753)₈

The solution for the given decimal number (263.87)₁₀ = (407.6753)₈

Example 3: Decimal to Hexadecimal number conversion

Convert (4356.763)₁₀ to hexadecimal number.

Solution.

Integer part conversion is done by successive division method.

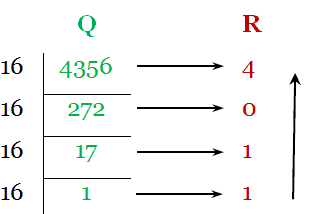
For Integer part, we get, (4356)₁₀ = (1104)₁₆

Fractional part conversion is done by successive multiplication method.

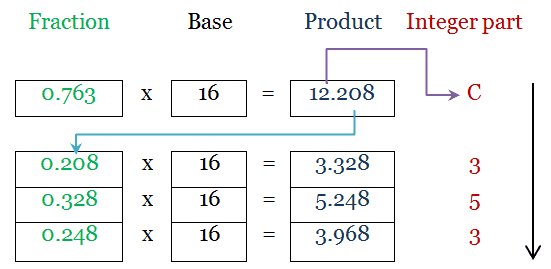
For Fractional part, we get, (0.763)₁₀ = (0.C353)₁₆

The solution for the given decimal number (4356.763)₁₀ = (1104.C353)₁₆

---

Binary to Octal Number conversion

• For this number system conversion, the base for binary number system is 2 and the base for octal number system is 8.
• The base for octal number is the third power of the base for binary number.
• So, group 3 bits of binary number, starting from LSB for integer part and start from MSB for fractional part. Add 0 at the end, if required.
• Write equivalent octal number for each group of 3 bits, to get its octal number.

Example: Convert (10100110.1101)₂ to its octal equivalent.

Solution.

In the given binary number, by grouping 3 bits starting from LSB for the integer part, we get 110, 100, 010. Similarly, grouping 3 bits starting from MSB for fractional part, we get 110, 100.

For the grouped bits, write the equivalent octal numbers to get the value. (Refer the relation between the different number system)

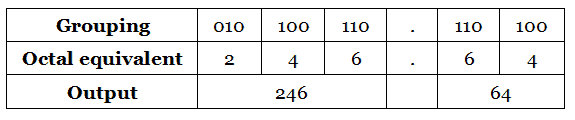
Thus the obtained octal number for (10100110.1101)₂ is (246.64)₈.

---

Octal to Binary Number conversion

For this conversion, perform the reverse process of binary to octal conversion. That is, each digit of the given octal number is individually converted into its binary equivalent to get the desired value. Let’s look at an example.

Example: Convert the octal number (242.35)₈ to its binary equivalent.

Solution. For each digit of the given octal number, write its binary equivalent to get the desired value.

Thus the obtained binary number for (242.35)₈ is (10100010.011101)₂.

---

Binary to Hexadecimal Number conversion

• For this number system conversion, the base for the binary number system is 2 and the base for the Hexadecimal number system is 16.
• The base for the hexadecimal number is the fourth power of the base for binary number.
• So, group 4 bits of a binary number, starting from LSB for the integer part and start from MSB for the fractional part. Add 0 at the end, if required.
• Write an equivalent hexadecimal number for each group of 4 bits, to get the hexadecimal number.

Example: Convert the binary number(1010011011.1101001)₂ to its hexadecimal equivalent.

Solution.

In the given binary number, by grouping 4 bits starting from LSB for the integer part, we get 1011, 1001, 0010. Similarly, grouping 3 bits starting from MSB for fractional part, we get 1101, 0010.

For the grouped bits, write the equivalent hexadecimal numbers to get the value. (Refer the relation between the different number system)

Thus the obtained hexadecimal number for (1010011011.1101001)₂ is (29B.D2)₁₆.

---

Hexadecimal to Binary Number conversion

For this conversion, perform the reverse process of binary to hexadecimal conversion. That is, each digit of the given hexadecimal number is individually converted into its binary equivalent to get the desired value. Let’s look at an example.

Example: Convert the hexadecimal number (689.2A)₁₆ to its binary equivalent.

Solution. For each digit of the given hexadecimal number, write its binary equivalent to get the desired value.

Thus the obtained binary number for (689.2A)₁₆ is (11010001001.0010101)₂.