BCD and Excess-3 codes

BCD Code

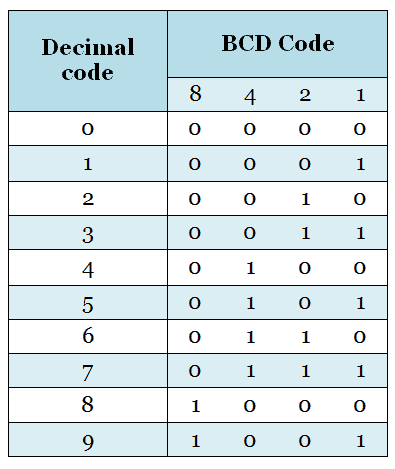
BCD code is an abbreviation for Binary coded Decimal codes. It is a numeric weighted code, in which each digit of a decimal number is represented by a separate group of 4-bits. There are several BCD codes like 8421, 2421, 3321, 4221, 5211, 5311, 5421, etc. The most common and widely used BCD code is 8421 code.

In 8421 code, the weights associated with 4 bits are 8, 4, 2, 1 from MSB to LSB. That is, the weight associated with 3rd bit is 8, the weight associated with 2nd bit is 4, the weight associated with 1st bit is 2 and the weight associated with 0th bit is 1. The following table shows the 8421 code for 0-9 decimal numbers.

BCD addition

When adding two BCD digits, three cases have to be considered.

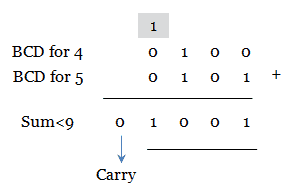
Case 1: Sum of two BCD digit equals or less than 9 with carry 0.

If the addition of two BCD digit produces an output which is equal to or less than 9 and there is no carry, then it is a valid BCD number. Let us learn this case from an example. Consider the addition of 4 and 5 in BCD.

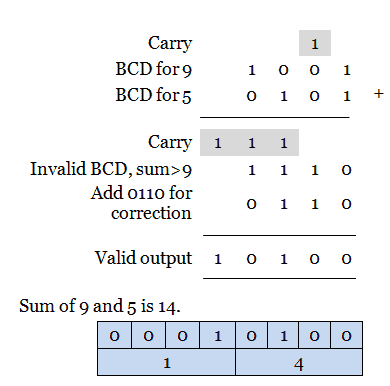
Case 2: Sum of two BCD digit is greater than 9 with carry 0.

If the addition of two BCD digit produces an output which is greater than 9 and there is a carry, then it is an invalid BCD number. To make it a valid number, add 0110(6) with the invalid result. Let us learn this case from an example. Consider the addition of 9 and 5 in BCD.

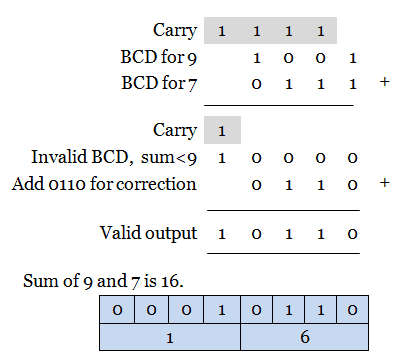
Case 3: Sum of two BCD digit equals or less than 9 with carry 1.

If the addition of two BCD digit produces an output which equals or less than 9 and there is a carry, then it is also an invalid BCD number. To make it a valid number, add 0110(6) with the invalid result. Let us learn this case from an example. Consider the addition of 9 and 7 in BCD.

Procedure for BCD addition

Considering all the above said three cases, the procedure for BCD addition can be summarized as follows.

• Add two BCD numbers using ordinary binary addition.
• If the sum is equal to or less than 9, no correction is needed to the result.
• If the sum is greater than 9 or if a carry is generated, the sum is said to be invalid.
• To make it valid, add 0110(6) to the sum. If carry results from it, add the carry to the next higher order BCD digit.

Problem : Add (35)₁₀ and (17)₁₀ in 8421 BCD.

BCD subtraction Using 9’s complement

Hint: 9’s complement is found by subtracting each digit in the given decimal number from 9.

Follow the below given procedure to subtract two numbers using 9’s complement.

• When subtracting two BCD numbers(A-B), find the 9’s complement of the negative decimal number(B).
• Add A+9’s complement of B.
• If carry is generated, add the carry to the result.
• If carry is not generated, find the 9’s complement to get the final result.

Problem : Subtract (56)₁₀ – (32)₁₀ in BCD using 9’s complement.

(56)₁₀ – (32)₁₀ = (24)₁₀

BCD subtraction Using 10’s complement

Hint: 10’s complement can be found by adding 1 with 9’s complement.

Follow the below given procedure to subtract two numbers using 10’s complement.

• When subtracting two BCD numbers(A-B), find the 10’s complement of the negative decimal number(B).
• Add A+10’s complement of B.
• If carry is generated, the obtained result is positive. Discard the carry to get the result.
• If carry is not generated, the obtained result is negative, find the 10’s complement to get the final result.

Problem : Subtract (35)₁₀ – (48)₁₀ in BCD using 10’s complement

(35)₁₀ – (48)₁₀ = (-13)₁₀

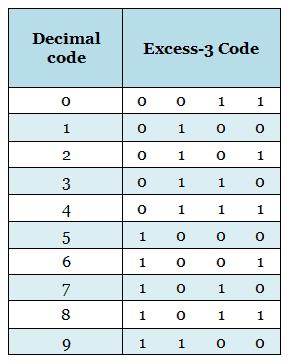
Excess-3 code

Excess-3 code is derived by simply adding 3 to each BCD number. It is a non-weighted code and it is a sequential code and reflective code.

Excess-3 addition

Follow the below steps to perform excess-3 addition

• Add two excess-3 numbers using binary addition method.
• If carry is generated, add 0011(3) to the result to get the final result.
• If carry is not generated, subtract 0011(3) to the result to get the final result.

Let us look at an example here. Add (5)₁₀ and (9)₁₀ in excess-3 code.

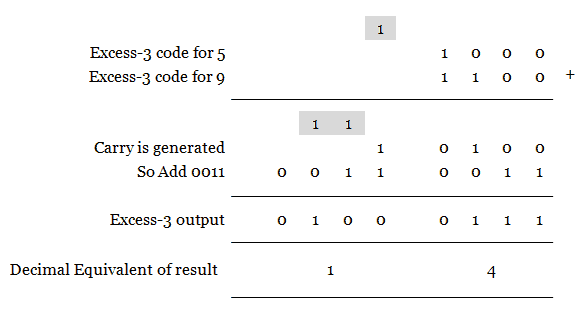
(5)₁₀ + (9)₁₀ = (14)₁₀

Excess-3 Subtraction

Follow the below steps to perform excess-3 subtraction

• While subtracting A-B, take the complement of B.
• Add A + complement of B.
• If carry = 1, add 0011 to the sum result.
• If carry = 0, subtract 0011 from the sum result.
• Add the carry with the next higher bit.

NOTE:

In excess-3 subtraction, If a carry is generated in the MSB, the obtained result(after following the above steps) is the final output. It is a positive result.

If the carry is not generated in the MSB, complement the result(obtained by following the above steps) to get the desired output. It is a negative result.

Let us look at some of the examples here.

Example 1: Subtract (5)₁₀ – (9)₁₀ in excess-3 code.

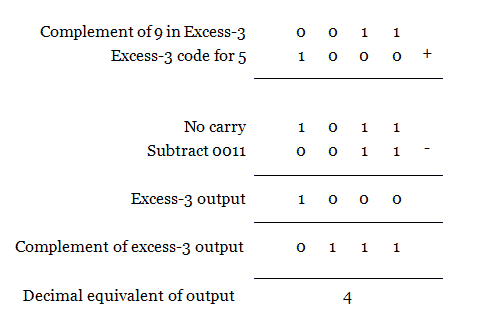
(5)₁₀ – (9)₁₀ = (-4)₁₀

Example 2: Subtract (9)₁₀ – (5)₁₀ in excess-3 code.

(9)₁₀ – (5)₁₀ = (4)₁₀

Example 3: Subtract (27)₁₀ – (18)₁₀ in excess-3 code.

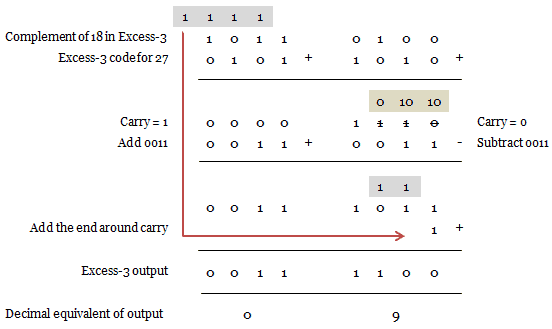
(27)₁₀ – (18)₁₀ = (9)₁₀

Example 4: Subtract (67)₁₀ – (79)₁₀ in excess-3 code.

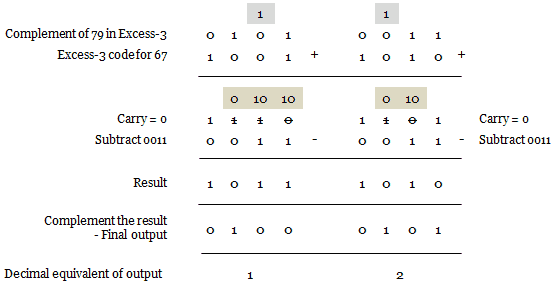
(67)₁₀ – (79)₁₀ = (-12)₁₀