What is mutually induced emf?

Inductance of a coil

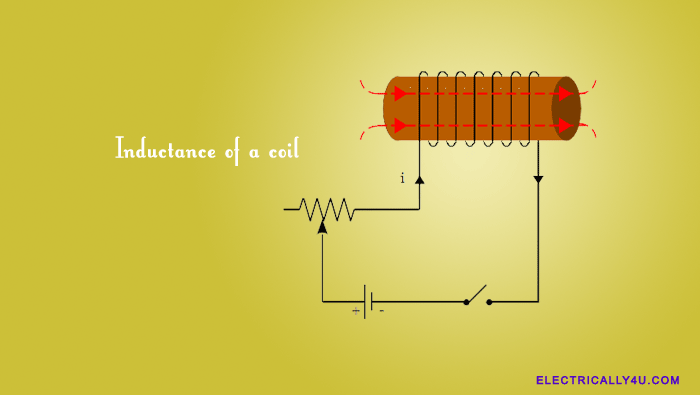
Inductance is the property of an inductor that opposes any change of current through the coil. An inductor has an important property: when the flux linking the coil changes, an emf is induced. It is also explained by Faraday’s law. In fact, this principle of inducing emf is fundamental to the operation of transformers, generators, and motors.

As per Lenz’s law, the direction of the induced emf is such that the current produced by it sets up a magnetic field opposing the cause that produces it. Hence, the voltage (e) induced is given by the expression,

$e = -N \frac{d \phi}{dt}$

where N is the number of turns, dϕ/dt is the rate of change of linking flux.

Types of Induced emf in inductor

EMF can be induced in two ways by varying the flux linking with the coil. They are

When a conductor is moved in a uniform magnetic field, an emf is induced. It is known as dynamically induced emf.
When an emf is induced by increasing or decreasing the magnitude of the current flowing through the coil. It is known as statically induced emf. In this case, there is no motion of the conductor or of the coil relative to the field.

Dynamically induced EMF

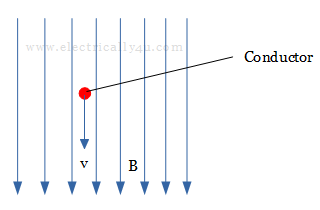
Let us consider a conductor of length l meters is placed in a uniform magnetic field of density B Wb/m². Let this conductor be moved in the direction of the field with a velocity of v m/s, as shown below. As you can see, no flux is cut by the conductor, therefore, no emf is induced in it.

Now consider that, if this conductor is moved in a direction perpendicular to the direction of the magnetic field with a velocity of v m/s. In this case, the flux is cut by the conductor, therefore, an emf is induced in the conductor. It is shown in the figure below.

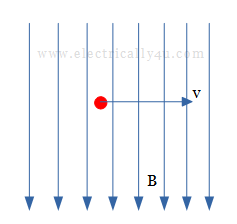
Area swept per second by the conductor = l x v m²/s

Flux cut per second = Flux density x area swept per second = Blv Wb/s

Flux cut per second is nothing but the rate of change of flux. Thus the induced emf is given by,

$e = \frac{d \phi}{dt} = Blv$

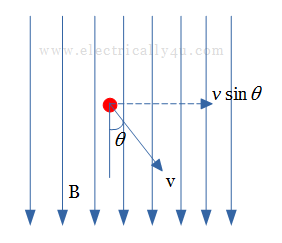
If the conductor is moved at an angle θ to the magnetic field, then the emf induced is proportional to the component of the velocity that is perpendicular to the magnetic field. The magnitude of induced emf is given by,

$\begin{align*} \small{ e = Blv \text{sin} \theta } \end{align*}$

The direction of induced emf is given by Fleming’s Right-Hand Rule.

Statically induced EMF

Statically induced emf is the emf induced by varying the current flowing through the coil. It is of two types: self-induced emf and mutually induced emf.

Self-induced EMF

When the emf is induced in the same circuit due to the changing current through the coil, then it is known as self-induced emf. The induced emf is also called the back emf or counter emf as its polarity is in the opposite direction to the applied voltage. The property of the coil that opposes any change in the current is called self-inductance.

Consider an inductor coil of N turns having a length of l meters, area of cross-section a m² and relative permeability of µ_r.

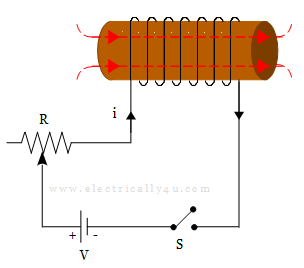
When a current of I amperes, a magnetic flux ϕ is set up around the coil, which is given by,

$\begin{align*} \small{ \phi = \dfrac{\text{MMF}}{\text{Reluctance}} = \dfrac{\text{NI}}{\text{S}} = \dfrac{\text{Ni}}{ l/ \mu _0 \mu _r a} } \end{align*}$

$\begin{align*} \small{\phi = \dfrac{Ni \mu _0 \mu _r a}{l} --->(1) } \end{align*}$

If the current flowing through the coil is changed, the flux produced by it changes and thus the emf is induced. The self induced emf is given by,

$e = -N \frac{d\phi}{dt} = -N \frac{d}{dt} \Bigg[ \frac{Ni \mu _0 \mu _r a}{l} \Bigg]$

$e = -N \frac{N \mu _0 \mu _r a}{l} . \frac{di}{dt} = - \frac{N^2 \mu _0 \mu _r a}{l}. \frac{di}{dt}$

$e = -L \frac{di}{dt}$

where L is a constant for any givn coil and is called the coefficient of self inductance. Its unit is measurd in Henry.

$L = \frac{N^2 \mu _0 \mu _r a}{l} \text{ Henry}$

If the number of turns of the coil and the fux produced for the amount of current flowing through the coil is known, the self inductance of the coil can be derived as follows.

$L = \frac{N^2 \mu _0 \mu _r a}{l} = \frac{N}{i} \frac{N \mu _0 \mu _r a}{l} i$

Using the equation (1), the self-inductance of the coil becomes,

$L = \frac{N \phi}{i} \text{weber-turns per ampere}$

Hence a coil is said to have a self-inductance of one henry, if a current of 1 A, whn flowing through it, produces flux linkage of 1 Wb-turn in it.

Mutually Induced EMF

Let us consider two coils A and B placed close to each together so that the flux created by one coil completely links with the other coil. A battery and switch S is connected to coil A. A galvanometer G is connected to the coil B as shown below.

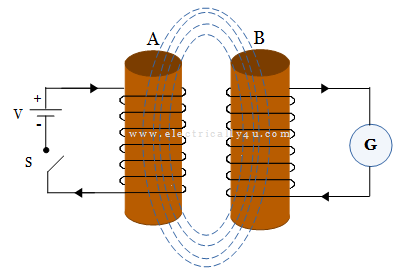
When switch S is opened, no current flows through the coil and hence no flux is linked with the coil. Thus no emf is induced in the other coil. If the switch S is closed, the current in the coil A starts to increase which produces a flux in the coil A. Therefore the flux linking with the coil B increases, and an emf is induced in the coil B. The induced emf is called mutually induced emf. It can be observed from the galvanometer deflection.

When the current through coil A becomes constant, the flux linking with the coil also becomes constant, and hence no emf is induced in coil B. So the pointer in the galvanometer returns back to the zero position.

Now, when the switch is opened, the current through coil A starts decreasing. Hence, the flux linking with coil B decreases and so an emf is induced in the opposite direction. It can also be observed from the galvanometer deflection.

Mutual inductance can be defined as the ability of one coil to induce an emf in a nearby coil when the current flowing in the first coil is changed. The value of mutual inductance is measured in terms of the coefficient of mutual induction M.

If all the dimensions of the coils are known, the coefficient of mutual induction can be determined using the formula,

$M = \frac{N_1 N_2 a \mu _0 \mu _r}{l} \text{ Henry}$

If the number of turns of the coil and the flux linking with this coil for the amount of current flowing through the other coil is known, the mutual inductance of the coil can be derived as follows.

$M = \frac{N_2 \phi _2}{i_1} \text{ Henry}$

When the magnitude of induced emf in the second coil for a given rate of change of current in the first coil is known, mutual inductance can be determined as below,

$M = \frac{e_m}{dI_1/dt} \text{ Henry}$

FAQs

Whenever the current in coil A changes, the flux linking with coil B changes, and an emf known as mutually induced emf is induced in coil B.

Inductance of a coil