Mutual Inductance and coupling coefficient
Mutual inductance is the basic operating principle of electrical machines such as transformers, motors, and generators. It is applied to any electrical component that needs interaction with another magnetic field. This principle is referred to as electromagnetic induction.
Mutual inductance is the ability of a coil to induce an emf in the nearby coil when the current flowing through the first coil is changed with respect to time.
As you know, the changing current in an inductor coil produces a changing magnetic flux around the coil. When a magnetic field exists in a circuit, there is a possibility that an emf will be induced in the other circuits linked by the field.
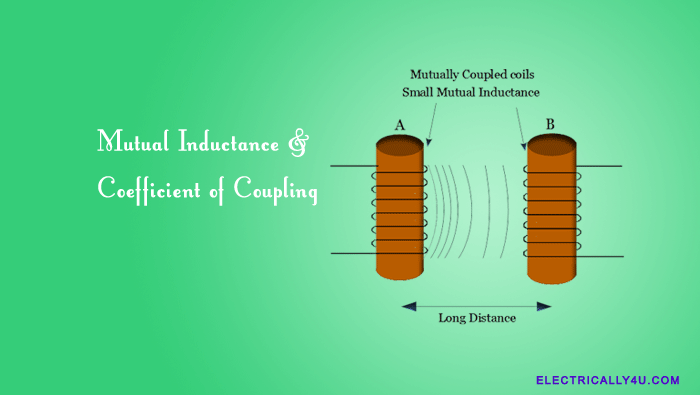
If two circuits are linked by the same magnetic field, they are said to be magnetically coupled. It is shown in the below figure.
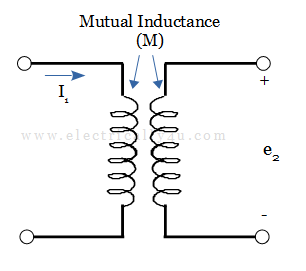
The circuit element used to represent magnetic coupling is known as mutual inductance. It is represented by the symbol M and is measured in Henry. The volt-ampere relationship is expressed as,
![\[e_2 = M \frac{di_1}{dt} \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-6424c116e5096f29054ce1116d80a417_l3.png "Rendered by QuickLaTeX.com")
Mutual Inductance between coils
The value of mutual inductance varies from one coil to another. It depends on the relative positioning of the two mutual inductor coils, as shown below.
If the primary coil (A) is placed at a shorter distance from the secondary coil (B), then nearly all of the magnetic flux generated by the first coil will interact with the second coil. Hence, a relatively large emf is induced and therefore produces a large mutual inductance value.
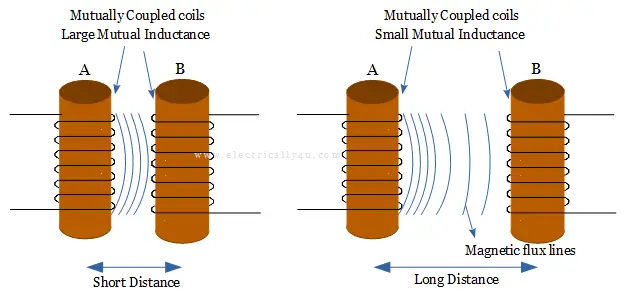
Similarly, if the two coils are placed at a larger distance from one another, the amount of magnetic flux linked with the second coil will be weaker. It produces a much smaller induced voltage and, therefore, a much smaller mutual inductance value.
So the effect of mutual inductance is very much dependent upon the relative positions or spacing of the two coils, and this is demonstrated below.
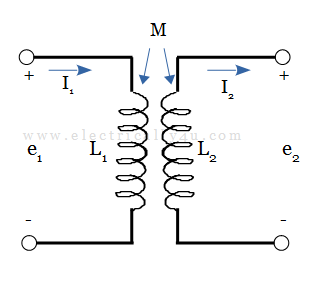
Consider two coils placed adjacent to each other. If current flows in both the coupled circuits, EMFs of self-inductance and mutual inductance are induced in each circuit. Each coil has its own self-inductance and mutual inductance, which indicates that they are coupled together.
The emf induced in coil 1 and coil 2 are given as follows.
![\[e_1 = L_1 \frac{di_1}{dt} + M \frac{di_2}{dt} \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-f7acc6e73d840a9edf4c669dfbfa8ede_l3.png "Rendered by QuickLaTeX.com")
![\[e_2 = L_2 \frac{di_2}{dt} + M \frac{di_1}{dt} \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-2fc0b303256fdce97a640d3ba478047e_l3.png "Rendered by QuickLaTeX.com")
In closely coupled electric circuits, the transfer of energy takes place through the medium of the mutual magnetic field. It is the basis for the operation of a transformer.
Coefficient of Coupling
When two coils are placed close to each other, the flux produced by one coil links with the other coil. But not all the flux links with the nearby coil, only a certain portion (say, K) of flux links with another coil. K is called the coefficient of coupling and its value varies between 0 and 1.
Flux created in coil A due to the flow of current i1,
![\[ \phi _1 = \frac{N_1 i_1}{l/ \mu _0 \mu _r a } \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-8eed9d873d236ab978080e4a762641e7_l3.png "Rendered by QuickLaTeX.com")
![\[ \phi _1 = \dfrac{\mu _0 \mu _r a N_1 i_1}{l} --->(1)\]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-19a25305770bb06990e3031f6b9e44fb_l3.png "Rendered by QuickLaTeX.com")
Flux linking with coil B,
![\[ \phi _2 = K \phi _1 = K \frac{\mu _0 \mu _r a N_1 i_1}{l} \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-90409f759cef04e7613ebf39cda00044_l3.png "Rendered by QuickLaTeX.com")
Coefficient of self-inductance of coil A,
![\[L_1 = \frac{N_1 \phi _1}{i_1} = \frac{\mu _0 \mu _r a {N_1}^2 }{l} --->(2) \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-c8fc48ddda560366fd0977bfa1030b81_l3.png "Rendered by QuickLaTeX.com")
Coefficient of self-inductance of coil B,
![\[L_2 = \frac{N_2 \phi _2}{i_2} = \frac{\mu _0 \mu _r a N_2^2 }{l} --->(3) \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-046a71f07ecbcd70a66a9aca061216bd_l3.png "Rendered by QuickLaTeX.com")
Coefficient of mutual inductance,
![\[M = \frac{N_2 \phi _2}{i_1} = \frac{K\mu _0 \mu _r a N_1 N_2}{l} --->(4)\]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-0ad0d470ae787d58e0bd01c9f46d4cac_l3.png "Rendered by QuickLaTeX.com")
Multiplying the equations (2), (3) and taking square root, we get,
![\[ \sqrt{L_1 L_2} = \frac{\mu _0 \mu _r a N_1 N_2}{l} \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-c64ac6bbb975fa16275742fe22687ff2_l3.png "Rendered by QuickLaTeX.com")
Using equation (4) in the above expression, we get
![\[ \sqrt{L_1 L_2} = \frac{M}{K} \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-66b6d61cfd9e7abe2dfce006b60e9829_l3.png "Rendered by QuickLaTeX.com")
![\[ M = K \sqrt{L_1 L_2} \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-47656f13e8bf408aa2a8de29501533d7_l3.png "Rendered by QuickLaTeX.com")
When the two coils are perfectly coupled, that is, when the flux due to one coil completely links with the other coil, the coupling coefficient, K is unity. Thus the mutual inductance M becomes,
![\[ M = \sqrt{L_1 L_2} \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-8a0d61714fa527562fa16a78c3e6f93c_l3.png "Rendered by QuickLaTeX.com")
If the two coils are tightly coupled, the value of the coefficient of coupling, K is greater than 0.5. When the flux due to one coil does not link with the other coil, the value of K will be zero.
Solved Problem
Calculate the coefficient of coupling having self-inductances of 50 mH and 60 mH. The mutual inductance between them is 30 mH.
Given. L1 = 50 mH, L2 = 60 mH, M = 30 mH
Solution.
We know the formula for Coeficient of coupling,
![\[ K = \frac{M}{\sqrt{L_1 L_2}} = \frac{30}{50 * 60} \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-655b554c1c70757b1b19173e7a7c39bb_l3.png "Rendered by QuickLaTeX.com")
K = 0.5477
Related Posts