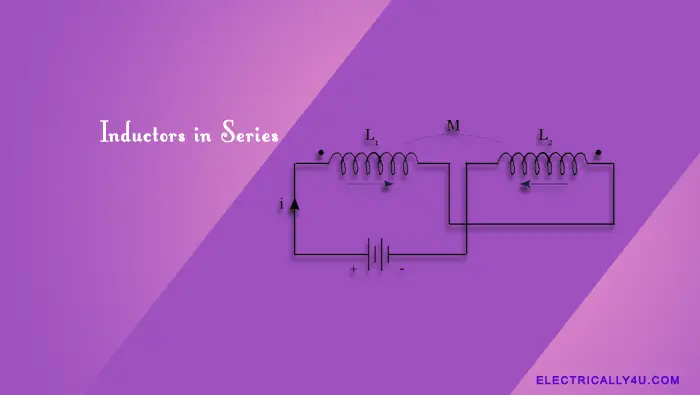
Inductors in Series

Inductors in series have a total inductance value that includes the effect of both the self-inductance and mutual inductance. An inductor is nothing but a coil of wire wound around a central iron core. It is a passive component that stores energy in the form of an electromagnetic field.

When a current I flows through the coil of wire, a magnetic flux ϕ is produced around the core, proportional to the flow of current. If so, the inductance of the coil is given by the ratio of flux produced to the current flowing through the coil.

$L = \frac{\phi}{I}$

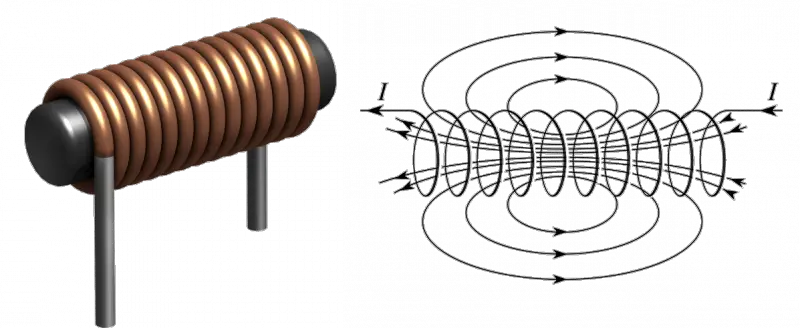
Inductance is the property of an inductor, which opposes the change in current through the coil. It is represented with the letter ‘L’ and the unit of inductance is Henry. The voltage across the inductor is proportional to the rate of change of current. It is expressed as,

$e \propto \frac{di}{dt}$

$e = L\frac{di}{dt}$

where L is the value of inductance in Henry.

Inductors in Series without mutual inductance

Consider three inductors L₁, L₂ and L₃ are connected in series as shown below. Let V be the supply voltage applied across the three series inductor and I be the current flowing through the circuit.

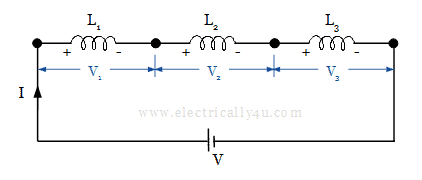
Each inductor carries the same amount of current I. Let V₁, V₂, V₃ be the voltage across the inductors L₁, L₂, L₃ respectively. So, we can write,

V = V₁ + V₂ + V₃ ——–> (1)

The voltage across each inductor is given by,

$V_1 = L_1 \frac{di}{dt}, V_2 = L_2 \frac{di}{dt}, V_3 = L_3 \frac{di}{dt}$

Thus equation (1) becomes

$V = L_1 \frac{di}{dt} + L_2 \frac{di}{dt} + L_3 \frac{di}{dt} = (L_1 + L_2 +L_3)\frac{di}{dt} --->(2)$

If L_eq is the effective inductance of the entire inductor circuit, then the voltage equation is given by

$V = L_{eq}\frac{di}{dt} --->(3)$

From equations (2) and (3), we can write,

L_eq = L₁ + L₂ + L₃

If ‘n’ number of inductors are connected in series, then the equivalent inductance is given by the expression,

$L_{eq} = L_1 + L_2 + L_3 + .... + L_n$

The effective or equivalent inductance of the inductor in a series is the sum of the inductances of individual inductors.

Inductors in Series with mutual inductance

When inductors are connected in series, the flux produced by one coil links with the other. Accordingly, the effect of mutual inductance either increases or decreases the total inductance depending upon the amount of magnetic coupling. The effect of this mutual inductance depends upon the distance between the coil and their orientation to each other.

Mutually connected series inductors can either aid or oppose the total inductance. If the magnetic flux produced by the current flows in the same direction, then the coils are said to be Cumulatively Coupled. If the current flows in the opposite directions then the coils are said to be Differentially Coupled.

Cumulatively coupled coils

Consider the below circuit, in which two inductors are wound on a common core. Both the inductors are connected in series and are cumulatively coupled. The current flow in the circuit enters the dot end of the coil and leaves at the other end. The effect of mutual inductance is taken into account.

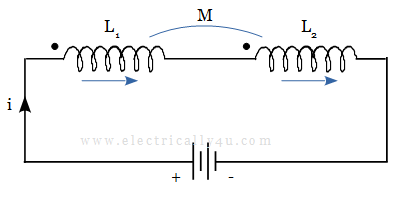
As the effect of mutual inductance is considered, the voltage drop across each inductor needs to be modified. The self-inductance of each inductor coil, L₁ and L₂ will be the same as before, but the mutual inductance, M will be added.

The emf induced in coil 1 is given as,

$e_1 = L_1 \frac{di}{dt} + M \frac{di}{dt} = (L_1 + M) \frac{di}{dt}$

Similarly the emf induced in coil 2 is given as,

$e_2 = L_2 \frac{di}{dt} + M \frac{di}{dt} = (L_2 + M) \frac{di}{dt}$

The total induced emf in the cummulatively coupled circuit is given as,

$e = e_1 + e_2 = (L_1 + L_2 + 2M) \frac{di}{dt}$

The total inductance of a cumulatively connected indcutor coil is given as,

$\frac{e}{di/dt} = L_1 + L_2 + 2M$

$L = L_1 + L_2 + 2M$

Differentially coupled coils

Consider the two inductor coils wounded in the common core as shown below. In this case, the current in coil 1 flows opposite to that of coil 2. Hence, the effect of mutual inductance in one coil cancels the effect in the other coil.

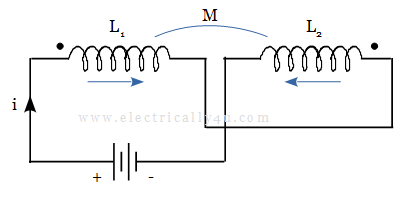
To take this canceling effect into account, a minus sign is used with M when the magnetic field of the two coils is differentially coupled.

The emf induced in coil 1 is given as,

$e_1 = L_1 \frac{di}{dt} - M \frac{di}{dt} = (L_1 - M) \frac{di}{dt}$

Similarly the emf induced in coil 2 is given as,

$e_2 = L_2 \frac{di}{dt} - M \frac{di}{dt} = (L_2 - M) \frac{di}{dt}$

The total induced emf in the differentially coupled circuit is given as,

$e = e_1 + e_2 = (L_1 + L_2 - 2M) \frac{di}{dt}$

The total inductance of a differentially connected indcutor coil is given as,

$\frac{e}{di/dt} = L_1 + L_2 - 2M$

$L = L_1 + L_2 - 2M$

Solved Problem

A primary coil having an inductance of 50 μH is connected in series with a secondary coil of 120 μH and the total inductance of the combination is measured to be 110 μH. Determine the coefficient of coupling.

Given.

Self-inductance of the coil 1, L₁ = 50 μH

Self-inductance of the coil 2, L₂ = 120 μH

Total inductance, L = 110 μH

Solution.

Since the total inductance (given value, L) is less than the arithmetic sum of the self-inductance of coils (L₁ and L₂), the coils have been connected in a way such that fluxes are opposing each other.

Hence the equivalent inductance is given by the relation,

$L = L_1 + L_2 - 2 M$