Inductors in Parallel

When inductors are connected in parallel, the voltage drop across each inductor would be the same. In the case of inductors in series, the equivalent inductance is obtained by adding the inductances of all the individual inductors connected in series. But for parallel connection of inductors, the equivalent inductance is calculated differently.

In the below section, the equivalent inductance of inductors connected in parallel is discussed, with and without considering the mutual inductance.

Inductors in Parallel without mutual inductance

Let us consider three inductors L₁, L₂ and L₃ are connected in parallel with one another. The supply voltage V is given across the parallel combination of three individual inductors. Since all the elements are in parallel branches, the voltage is the same between points 1 and 2.

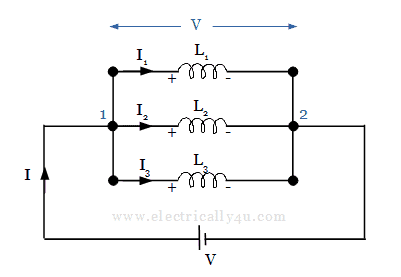
Let I be the current flowing from the supply. This current has three paths along L1, L2, L3 from node point 1, so the corresponding currents are I₁, I₂, I₃, as shown in the figure.

The current through the parallel inductor is written as,

The current through each inductor is given by,

Now, equation (4) becomes,

If L_eq is the equivalent inductance of the entire circuit, then the total current in the electrical circuit is given by,

From equation (5) and (6), we can write,

If there are n number of inductors connected in parallel, then the equivalent inductance or effective inductance formula is given by,

Thus the total equivalent inductance of inductors connected in parallel is equal to the sum of the reciprocal of each individual inductance L₁, L₂, … L_n.

Inductors in Parallel with mutual inductance

When inductors are connected in parallel, the magnetic field produced by one coil links with the other. Accordingly, the effect of mutual inductance either increases or decreases the total inductance depending upon the amount of magnetic coupling. The effect of this mutual inductance depends upon the distance between the coil and its orientation to each other.

Similar to the inductors in series, mutually connected parallel inductors can either aid or oppose the total inductance. The magnetic flux produced by the current flows in the same direction in a parallel aiding connected coils. In the case of parallel opposing connected coils, the current flows in opposite directions.

Parallel aiding inductor coils

Consider the below circuit, which shows the parallel connection of two inductors. The current enters the dot end of the coil and leaves at the other end. The effect of mutual inductance is taken into account. The flux produced by one coil adds to the other coil, hence the total flux produced increases.

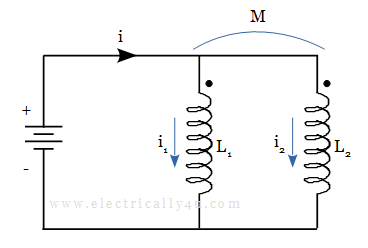
As the effect of mutual inductance is considered, the voltage drop across each inductor needs to be modified. We know that the voltage across the parallel circuit would be the same. In the above circuit, the two currents, i₁ and i₂ must vary so that the voltage across the inductors stays the same.

The total inductance of inductor in parallel aiding coils is given as,

If the mutual inductance between the parallel-connected inductor coil is zero, the equivalent inductance would be the same as that of two self-induced inductors in parallel.

If the inductances of two inductors are equal and there exists a perfect magnetic coupling, then the equivalent inductance is given by L as L₁ = L₂ = M.

Parallel opposing inductor coils

Consider the two inductor coils connected in parallel as before except that, one coil is reversed with respect to the other. It is shown in the figure below. In this case, the current in coil 1 flows opposite to that of coil 2.

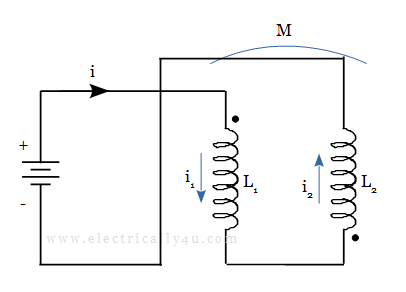
The flux produced by one coil opposes the flux produced in the other coil, hence the total flux produced decreases. Hence, the effect of mutual inductance in one coil cancels the effect in the other coil.

The total inductance of parallel opposing connected coils is given by,

If the inductances of two inductors are equal and there exists a perfect magnetic coupling, then the equivalent inductance will be zero. It is because the two inductors cancel out each other.

Solved Problem 1

Let us solve a problem to calculate equivalent inductance of the given circuit.

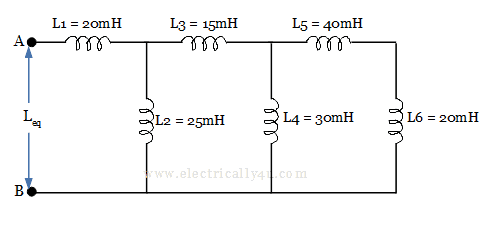
In the above example, inductor L4 is in parallel with a series combination of L5 and L6. The equivalent inductance value of these three inductors L4, L5 and L6 are

Now, the circuit get reduced as below,

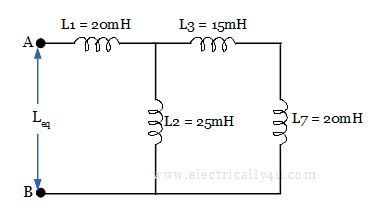
If you look at the circuit, inductor L2 is in parallel with the series combination of inductors L3 and L7. The corresponding equivalent inductance value is

Again the circuit is reduced as below,

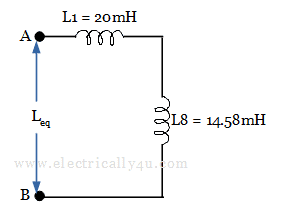
In the reduced circuit, the inductors L1 and L8 are in series.

Thus the equivalent inductance is given by,

When two inductors are connected in either series or parallel, the magnetic flux produced from one inductor will link with the other inductor. This property is called as mutual inductance.

Solved Problem 2

Two coils of self-inductance 100 mH and 220 mH and mutual inductance of 80 mH are connected in parallel. Determine the equivalent inductance of combination if (i) mutual flux helps the individual fluxes and (ii) mutual flux opposes the individual fluxes.

Given.

Self-inductance of the coil 1, L₁ = 100 mH = 0.1 H

Self-inductance of the coil 2, L₂ = 220 mH = 0.22 H

Mutual inductance, M = 80 mH = 0.08 H

Solution

(i) Equivalent inductance of combination if mutual flux helps the individual fluxes (parallel aiding coils)

(ii) Equivalent inductance of combination if mutual flux opposes the individual fluxes (Parallel opposing coils)