Torque equation of a DC Motor with solved problem

The torque equation of dc motor is essential for analyzing the rotating force of a motor. A torque is nothing but the turning or twisting moment of a force about an axis.

It is measured by the product of force and the radius at which the force acts. Newton-metre(Nm) is the unit of torque.

Let us consider a pulley or a wheel with a radius of r metre. When a circumferential force of F newton acts upon the pulley, it will cause the pulley to rotate at N rpm.

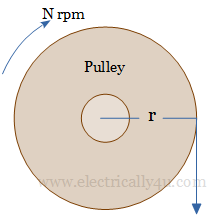
Torque is given by the formula, T = Force * radius.

Work done by the pulley = force * distance moved.

Work done by the pulley = F * 2πr joule

Power developed = F * 2πr * N Joules/second or Watts

Power developed = (F * r) * 2πN

where 2πN is the angular velocity ω in radians/second

Therefore, Power developed, P = T * ω watts

   

Torque developed in motor armature

Let us derive the torque equation of dc motor. Assume T_a be the torque developed in the armature of a motor running at N rpm.

   

We have derived the power equation of a dc motor, where

   

Equating the equations (1) & (2), we get,

   

   

   

We know the equation of back emf of a dc motor. It is given by,

   

Substituting the above back emf equation in equation (3), we get

   

   

From the above torque equation of a motor armature, we can say that, the armature torque,

T_a α φI_a

In the case of a series motor, the flux produced in the field winding(φ) is proportional to the armature current(I_a), hence, T_a α I_a².

In the case of the shunt motor, the flux (φ) produced is practically constant. Hence T_a α I_a.

Shaft torque

All the torque(as calculated above) developed in the motor armature is not available for doing useful work. It is because some torque is needed for supplying the iron and friction losses in the motor.

The torque that is available for the dc motor to do the useful work is known as shaft torque(T_sh) in dc motor. The name indicates that the torque is available at the motor shaft.

Using the power developed equation, the motor output power is given by,

   

   

   

   

The difference between the armature torque(T_a) and the shaft torque(T_sh) is known as the lost torque due to iron and frictional losses of the motor. There are different methods of speed control of dc motor is available to achieve variable speeds.

Solved Problem #1

Let us take a look at some problem.

A 220 V, 4-pole series motor with 600 conductors wave-connected supplying a load of 7.5kW by taking 35 A from the motors. Calculate the developed torque and shaft torque, if the flux per pole is 15 mWb and its armature circuit resistance is 0.5 Ω.

Given Values: V = 220 v, No. of poles = 4, Z = 600, Wave-connected(A=2), Output power = 7.5 kW = 7500 W, Ia = 35 A, φ = 15 mWb = 0.015 Wb, R_a = 0.5 Ω

To Find : T_a and T_sh

Solution:

Developed torque is given by,

   

   

   

Back emf is given by,

   

Now, We know

   

   

   

Shaft torque is given by,

   

   

   

Solved Problem #2

A 440 V, 14 poles lap wound dc shunt motor takes 1550 A from the supply. There are 280 conductors. The effective diameter of the armature is 1.3 m and the active length of each conductor is 0.33 m. The value of average flux density is 0.7 T. Calculate the value of torque developed and speed of the motor.

Given Values: V = 220 v, No. of poles = 14, Z = 280, lap-wound(A=P), D = 1.3 m, l = 0.33 m, B_av = 0.7 T

To Find : T_a and N

Solution:

Flux per pole,

   

Neglecting the shunt field current and voltage drop in the armature, the back emf developed is obtained as,

   

Developed torque is given by,

   

   

   

Speed of the motor,