Voltage Equation and Power Equation of a DC Motor

In a dc motor, the applied input is electrical energy. The motor converts the electrical input into mechanical input. The applied voltage at the armature terminals of a DC motor has to overcome the back emf and has to supply the armature resistance drop.

Consider the following circuit of DC shunt motor, where V is the supply voltage, E_b is the back emf, I_a is the armature current and R_a is the armature resistance.

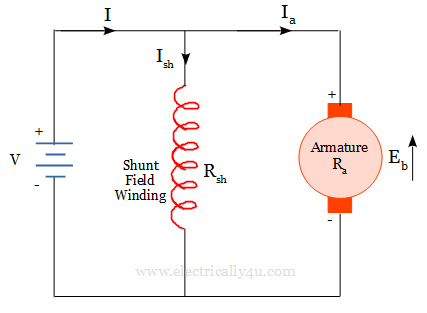
By applying KVL to the loop shown in the circuit, the voltage equation can be written as,

$\boxed { V = E_b + I_aR_a } --->(1)$

The above equation(1) is called the voltage equation of DC motor.

Power equation of DC motor

By multiplying the above equation by I_a on both sides, we get

$\boxed {VI_a = E_bI_a + {I_a}^2 R_a} --->(2)$

Equation(1) is the power equation of DC motor.

Here, VI_a = Electrical power input to the motor(armature input).

E_bI_a = Electrical equivalent of mechanical power developed in the armature.

I_a² R_a = Copper loss in the armature winding.

The power equation indicates that the input power is wasted as loss in the armature winding and the rest is converted into mechanical power.

The efficiency of a DC motor is the ratio of output power to input. It is given as,

$Efficiency = \frac{output power}{Input power} = \frac{E_bI_a}{VI_a} = \frac{E_b}{V}$

It indicates that, higher the value of back emf, higher the motor eficiency.

Condition for Maximum Power

From equation(2), the gross mechanical power developed by the armature is given by,

$P_m = VI_a - {I_a}^2 R_a$

To obtain the maximum power, differentiating the above equation with respect to I_a and equate it to zero,

$\frac{dP_m}{dI_a} = 0$

$V - 2I_aR_a = 0$

$I_aR_a = \frac{V}{2}$

Substituting in Equation(1),

$V = E_b + I_aR_a$

$V = E_b + \frac{V}{2}$

$\boxed{ E_b = \frac{V}{2} }$

This is the condition for maximum power developed in the motor armature. It depicts that the gross mechanical power developed by a motor is maximum when back emf is half the applied voltage. However this will not be applicable in real practice.

Let us solve a problem.

A 400V shunt motor has an armature resistance of 0.7 Ω and field resistance of 150 Ω. Determine the back emf when giving an output of 7 kW at 75% efficiency.

Given parameters: Input voltage(V_in) = 400 V, R_a = 0.7 Ω, R_sh = 150 Ω, Output power(P_o) = 7 kW, Efficiency = 75%

To find: Back emf(E_b)

Solution :

$Efficiency = \frac{output power}{Input power}$