Voltage regulation of transformer
The voltage regulation of transformer is used to understand the characteristics of transformer under loaded conditions. When a transformer is loaded with constant primary voltage, the secondary voltage decreases because of load current, internal resistance, and leakage reactance. The change in secondary voltage from no-load to full load at constant frequency and voltage is known as voltage regulation of transformer. It is usually expressed as a percentage of the rated terminal voltage.
If V2 is the secondary terminal voltage at full load and E2 is the secondary terminal voltage at no load. Then the percentage regulation of transformer is given by,
![\[ Voltage Regulation = \frac{E_2 - V_2}{E_2} \times 100 \]](https://sf.ezoiccdn.com/ezoimgfmt/electrically4u.com/wp-content/ql-cache/quicklatex.com-b84d213b9d53d850c72aa54c07f22061_l3.png "Rendered by QuickLaTeX.com")
It is also called as ‘down-regulation’. If the change in voltage from no-load to full-load is divided by full-load secondary terminal voltage, it is known as ‘up regulation’.
![\[ Voltage Regulation = \frac{E_2 - V_2}{V_2} \times 100 \]](https://sf.ezoiccdn.com/ezoimgfmt/electrically4u.com/wp-content/ql-cache/quicklatex.com-ff50fd91028a0337bfc8778499001a93_l3.png "Rendered by QuickLaTeX.com")
However, unless stated otherwise, down-regulation is considered as the voltage regulation of transformer.
Voltage regulation of transformer referred to primary values
The voltage regulation of transformer can also be explained in terms of primary values. In the simplified equivalent circuit of transformer, as shown in the figure below, the secondary no-load terminal voltage as referred to primary is V1 and the secondary full load voltage as referred to primary is V2‘. Then the percentage regulation of transformer is given as,
![\[ Voltage Regulation = \frac{V_1 - {V_2}^{'}}{V_1} \times 100 --->(1)\]](https://sf.ezoiccdn.com/ezoimgfmt/electrically4u.com/wp-content/ql-cache/quicklatex.com-08061f83a1d5805e2eb2ea00408cfa08_l3.png "Rendered by QuickLaTeX.com")
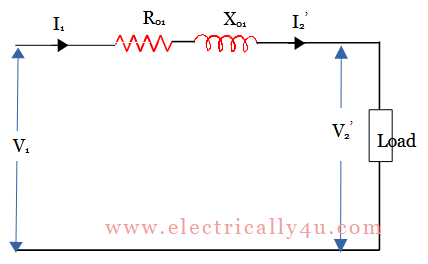
From its phasor diagram, as shown below for pure inductive load, the voltage relationship between V1 and V2‘ can be written as below. (Refer: Equivalent resistance and reactance of transformer to understand the phasor diagram and voltage equations)
V1 = V2‘ + I1R01 cos Φ + I1X01 sin Φ
V1 – V2‘ = I1R01 cos Φ + I1X01 sin Φ
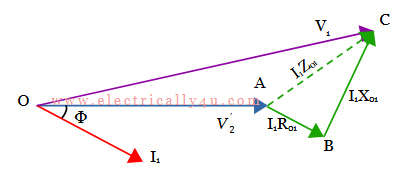
Equation(1) becomes,
![\[ Voltage Regulation = \frac{I_1R_{01} cos \phi +I_1X_{01} sin\phi}{V_1} \times 100 --->(2) \]](https://sf.ezoiccdn.com/ezoimgfmt/electrically4u.com/wp-content/ql-cache/quicklatex.com-a44763dcb9d692e09f2aa5c301ba8546_l3.png "Rendered by QuickLaTeX.com")
The above equation is the voltage regulation of transformer with pure inductive load.
For a pure capacitive load, the phasor diagram can be drawn as below, which has a leading power factor. Hence the current I1 leads the voltage V2‘. In this case, the voltage relation becomes,
V1 – V2‘ = I1R01 cos Φ – I1X01 sin Φ
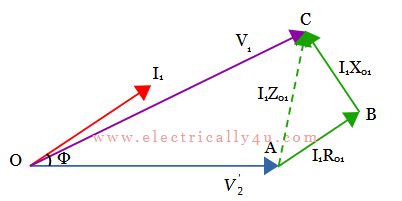
The voltage regulation of transformer for capacitive load is,
![\[ Voltage Regulation = \frac{I_1R_{01} cos \phi - I_1X_{01} sin\phi}{V_1} \times 100\]](https://sf.ezoiccdn.com/ezoimgfmt/electrically4u.com/wp-content/ql-cache/quicklatex.com-e80e35fe598b04f19e694e4074240a6a_l3.png "Rendered by QuickLaTeX.com")
For pure resistive load, the phasor diagram is drawn as below, which has a unity power factor. Hence the current I1 is in phase with the voltage V2‘. In this case, the voltage relation becomes,
V1 – V2‘ = I1R01
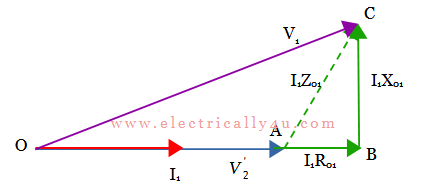
The voltage regulation of transformer for pure resistive load is,
![\[ Voltage Regulation = \frac{I_1R_{01}}{V_1} \times 100\]](https://sf.ezoiccdn.com/ezoimgfmt/electrically4u.com/wp-content/ql-cache/quicklatex.com-8e01b31fc10425eef1ed7b76e66ad2b3_l3.png "Rendered by QuickLaTeX.com")
Condition for zero regulation
The voltage regulation of tansformer will be zero if the numerator is zero in Equation(2).
I1R01 cos Φ +I1X01 sin Φ = 0
I1X01 sin Φ = – I1R01 cos Φ
![\[ \frac{sin \phi}{cos \phi} = - \frac{R_{01}}{X_{01}} \]](https://sf.ezoiccdn.com/ezoimgfmt/electrically4u.com/wp-content/ql-cache/quicklatex.com-5f325e69daba802565f054c54b6ac344_l3.png "Rendered by QuickLaTeX.com")
![\[tan \phi} = - \frac{R_{01}}{X_{01}} \]](https://sf.ezoiccdn.com/ezoimgfmt/electrically4u.com/wp-content/ql-cache/quicklatex.com-3ade04313652ac962735b7e24523bfea_l3.png "Rendered by QuickLaTeX.com")
The negative sign indicates that zero regulation occurs at the leading power factor.
Condition for Maximum regulation
The voltage regulation of tansformer will be maximum, if d/dΦ(regulation) = 0
![\[ \frac{d}{d\phi} \big(\frac{I_1R_{01} cos \phi +I_1X_{01} sin\phi}{V_1}\big) = 0 \]](https://sf.ezoiccdn.com/ezoimgfmt/electrically4u.com/wp-content/ql-cache/quicklatex.com-3a7a29e9e3cedf81d471220f140c41f6_l3.png "Rendered by QuickLaTeX.com")
![\[- \frac{I_1R_{01} sin\phi}{V_1} + \frac{I_1X_{01} cos\phi}{V_1} = 0\]](https://sf.ezoiccdn.com/ezoimgfmt/electrically4u.com/wp-content/ql-cache/quicklatex.com-f466bbb8ea63aac5838380ec1700db0c_l3.png "Rendered by QuickLaTeX.com")
![\[tan \phi} = \frac{X_{01}}{R_{01}} \]](https://sf.ezoiccdn.com/ezoimgfmt/electrically4u.com/wp-content/ql-cache/quicklatex.com-9f8c568583f5800852d70f6b8fea308a_l3.png "Rendered by QuickLaTeX.com")
It implies that maximum regulation occurs at lagging power factor.
Solved Problem 1
Determine the voltage regulation of transformer whose ohmic resistive drop is 2% and reactance drop is 7% at 0.8 p lagging.
Given data, Resistance drop = 2%, reactance drop = 7%
Solution:
The voltage regulation is given by the formula,
![\[ Voltage Regulation = \frac{I_1R_{01} cos \phi +I_1X_{01} sin\phi}{V_1} \times 100 \]](https://sf.ezoiccdn.com/ezoimgfmt/electrically4u.com/wp-content/ql-cache/quicklatex.com-1261a7969ca7e228c8e9f868271783c9_l3.png "Rendered by QuickLaTeX.com")
![\[ = \frac{I_1R_{01}}{V_1} \times 100 cos \phi + \frac{I_1X_{01}}{V_1} \times 100 sin\phi \]](https://sf.ezoiccdn.com/ezoimgfmt/electrically4u.com/wp-content/ql-cache/quicklatex.com-24c18ad18ce0441197c4b269f52f8ebb_l3.png "Rendered by QuickLaTeX.com")
![\[ = \% R cos \phi + \% X sin \phi = 2\times 0.8 + 7\times 0.6 \]](https://sf.ezoiccdn.com/ezoimgfmt/electrically4u.com/wp-content/ql-cache/quicklatex.com-d61626a4f6c648e0907bcab818e7b939_l3.png "Rendered by QuickLaTeX.com")
![\[ = 5.8 \% \]](https://sf.ezoiccdn.com/ezoimgfmt/electrically4u.com/wp-content/ql-cache/quicklatex.com-b113c959143763bc9b4e441e41db6c8c_l3.png "Rendered by QuickLaTeX.com")
Related Posts