Equivalent circuit of transformer

The equivalent circuit of transformer is a circuit representation of equations that describes the performance of the device. The equivalent circuit of transformer is used to predetermine the behavior of the transformer under various operating conditions. It can be drawn if the equations describing its behavior are known.
The voltage equations derived in the phasor diagram of a practical transformer, E2 = V2 + I2R2 + jI2X2 and V1 = -E1 + I1R1 + jI1X1 describe the transformer’s performance under load and help arrive at the transformer equivalent circuit. From these equations, it is understood that the equivalent circuit of transformer consists of a combination of resistances, inductances, voltage, etc.
The equivalent circuit of a transformer having a transformation ratio K = E2/E1 is shown in the figure below.
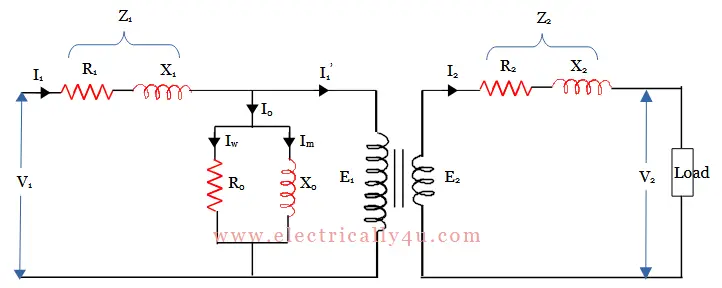
Under the no-load condition, the applied voltage in primary winding V1 gets dropped resulting in a reduction of primary induced emf E1. This is because the no-load current I0 is responsible for the production of iron loss and magnetic flux in the core. The effect of iron loss is represented by pure resistance R0 and magnetic flux is represented by pure reactance X0, both connected in parallel across the primary.
The value of R0 and X0 can be calculated as, R0 = E1 / Iw and X0 = E1 / Im, where Iw and Im are the working (or iron loss) component and magnetizing component respectively.
Equivalent circuit of transformer referred to primary
To obtain the equivalent circuit of transformer referred to as primary, all the parameters such as voltage, current, resistance, and reactance in the secondary side are transferred to the primary side using the transformation ratio(K), as shown in the figure below.
While transferring the secondary parameters to the primary side, it is important to note the equivalent resistance and reactance referred to primary, where the resistances and reactances are divided by K2, voltages are divided by K, and currents are multiplied by K.
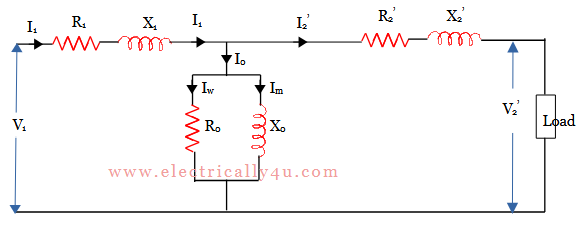
In the above circuit,
![]()
![]()
![]()
![]()
![]()
Since the no-load current is only 3-5% of the rated primary current. So I2‘ is approximately equal to I1. Hence the equivalent circuit can be simplified by transferring the exciting branch(R0 and X0) to the left position of the circuit, as shown below. It can be called an approximate equivalent circuit of transformer.
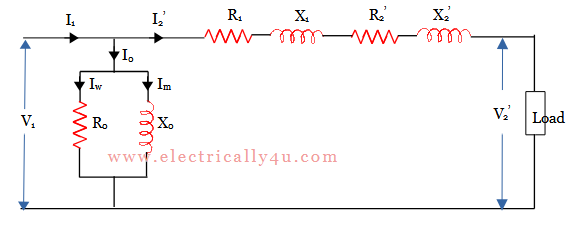
The above circuit can be further simplified by combining the resistance and reactances, i.e., R01 = R1 + R2‘ and X01 = X1 + X2‘. Here Z01 = R01 + jX01. The magnitude of impedance can be calculated as,
![]()
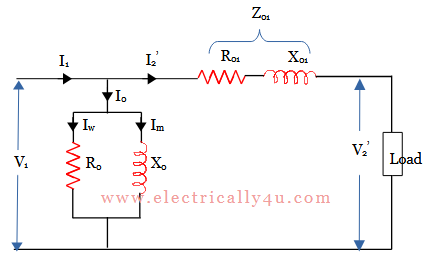
Since the no-load current is very small, removing the parallel branch from the exact equivalent circuit will not include any significant error in the behavior of the transformer under the loaded condition.
Thus further simplification is done to the equivalent circuit of transformer by neglecting the parallel branch consisting of R0 and X0. The simplified circuit is redrawn as follows.
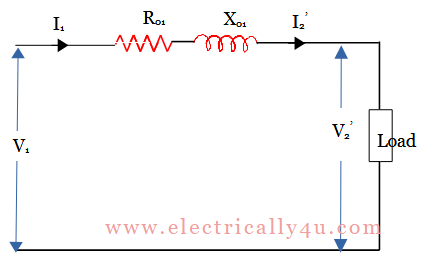
Equivalent circuit of transformer referred to secondary
Similarly, the exact equivalent circuit of transformer referred to as secondary can be obtained in the same way, which is drawn below.
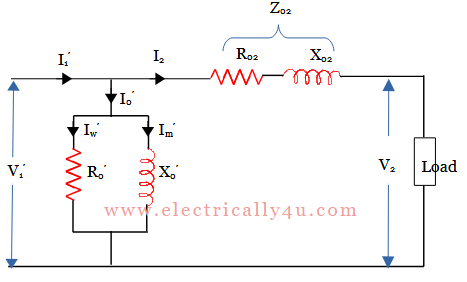


Related Posts