Current Divider Rule
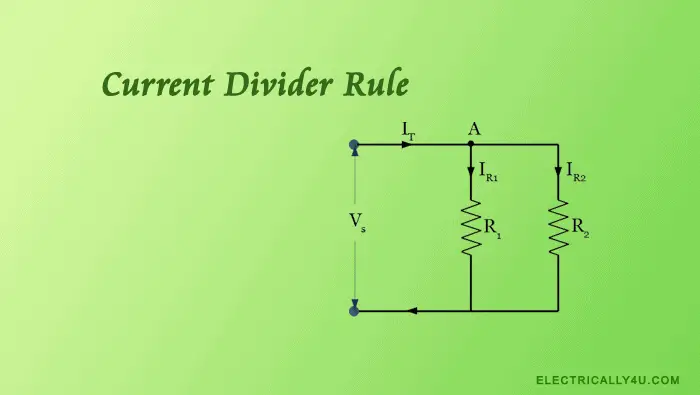
The Current Divider Rule is applicable to parallel circuits, in which the current is divided into the number of parallel branches. The current in each branch may have a different value depending on the specification of branch component.
In a parallel circuit, the current has different paths to flow but the voltage across each parallel branch is always equal. So the current divider rule explains how the current is divided among the parallel branch.
Current divider circuit
Let us consider a parallel circuit as shown below, which has two resistors R1 and R2 connected across the supply voltage Vs. Let IT be the total current flowing in the circuit, which has two parallel paths via resistor R1 and R2. IR1 is the current flowing through R1 and IR2 is the current flowing through R2.
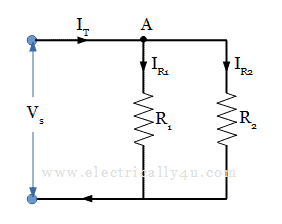
By Ohm’s Law, the voltage across the resistors R1 and R2 can be written as
![]()
![]()
At node A, by applying Kirchoff’s Current Law, the total current in the parallel circuit can be written as,
![]()
![]()
![]()
From equation (1), the current IR1 through the parallel branch R1 is obtained as below,
![]()
![]()
Similarly,from equation (2), the current IR2 through the parallel branch R2 is obtained as below,
![]()
![]()
Solved Problem 1
Consider two parallel resistors 25Ω and 15Ω are connected across the supply voltage of 40 V. Find the current flowing through each resistor and the total current supplied by the source.
In the given problem, R1 = 25 Ω and R2 = 15 Ω, Vs = 40 V.
The current flowing through each resistor is obtained as,
![]()
![]()
The total current is obtained as,
![]()
Solved Problem 2
In the following circuit, calculate the current flowing through each resistor and the total current flowing.
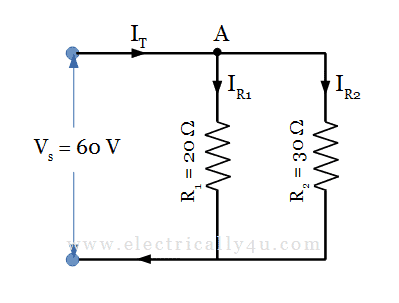
To find the total current, the equivalent resistance for the parallel circuit is obtained as,
![]()
The total current in the circuit is
![]()
By current division rule, the current through the resistor R1 and R2 is
![]()
![]()


Related Posts