Effect of Load on Synchronous Motor

The synchronous motor runs at a synchronous speed, which depends on the supply frequency. The operation of a synchronous motor is unique when compared to that of a DC motor and induction motor.

In dc motor or induction motor, an increase in load will drop the speed. It is because the load torque will be more than the torque produced by the motor. Hence to produce more torque and to satisfy the load, the motor draws more current from the supply. However, the speed of the motor reduces with an increase in load current.

In the case of a synchronous motor, the speed never drops irrespective of the load. That is the reason, this motor is unique in its operation.

Before understanding the behavior of the synchronous motor, you have to be clear with the working of DC motors.

Consider the case of a dc motor. During the motoring operation, back emf is developed in the armature of the motor. As per Lenz’s law, the developed back emf opposes the supply voltage. Thus the net voltage across the armature will be (V – E_b). It causes an armature current Ia to flow in the motor. It is given by,

   

where R_a – armature circuit resistance.

The back emf is given by the formula,

   

From the above expression, it is clear that the back emf depends on the speed of the machine.

Back emf in a synchronous motor

In a synchronous motor, the armature conductor is stationary and flux is rotating. Thus the flux produced by the rotating rotor winding is cut by the stationary armature conductors. Due to this, an emf is induced in the stator which according to Lenz’s law opposes the supply voltage. This induced e.m.f. is called back e.m.f. in a synchronous motor. 

The induced back emf is alternating in nature and is given by the equation,

E_b = 4.44 Kp Kd Φ f T volts

In the above equation, the frequency is constant, as it depends on the applied voltage. The other terms in the equation are constant, except flux produced. Hence the back e.m.f. can be controlled by changing the flux produced by the rotor winding.

Thus, it can be concluded that the synchronous motor depends on the excitation given to the field winding and not on the speed, as speed is always constant.

Since the construction of synchronous motor is the same as that of the alternator, the stator has a synchronous impedance, given by

Z_s = R_a + jX_s  

Where R_a is the stator winding resistance and X_s is the synchronous reactance. All the values are generally expressed on a per-phase basis.

So similar to the d.c. motor, we can write voltage equation for a synchronous motor as,

   

Here, V is the input voltage per phase and E_b is the induced back-emf per phase.

Synchronous motor on No-load

Let us consider the motor is operated at no-load condition. Assume the ideal condition, that is the motor has no losses.

Since there is no load and no losses, the armature current will be zero. Hence, there will not be any stress for the rotor to rotate. In this condition, the magnetic locking between the stator field and rotor field will be established in such a way that, both the magnetic axes coincide with each other.

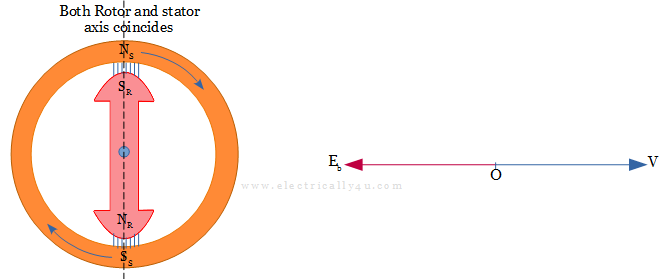
As the armature current is zero, the voltage equation will become, V = E_b.

The back emf E_b is equal and opposite to the supply voltage V as shown in the above phasor diagram.

However, this condition is not possible in practical conditions. Because the motor has a mechanical loss, iron loss, and a small amount of copper loss even in no-load condition.

Synchronous motor on No-load with losses

Let us consider the motor is operated at no-load condition. Assume the practical or real case, which means the motor losses are considered.

Dues to the losses, the rotor and stator axis do not coincide with each other. Instead, the rotor axis falls behind the stator axis by an angle δ. It is called load angle or power angle or coupling angle or angle of retardation or torque angle δ.

It causes a voltage E_R across the armature circuit and the motor draws no-load current from the mains. This no-load current lags behind the resultant voltage by an angle θ.

However, magnetic locking still exists between the magnetic fields of the rotor and stator. As a result, the rotor rotates at constant synchronous speed with a rotating magnetic field while maintaining an angle difference between the axes of the two fields, as illustrated in the figure below. Because of the rotor axis retardation, the flux lines between the two become stretched.

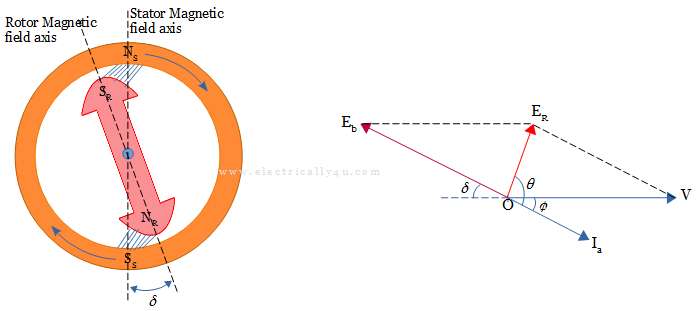
In this case, the magnitude of supply voltage and induced back emf will be the same but they will not be in exact opposition. Rather, it is displaced from its position by an angle δ.

Thus the vector difference between the input voltage and back emf is not zero but gives rise to a resultant phasor E_R as shown.

V – E_b = I_a Z_s = E_R

Under the no-load condition, δ is very small and hence E_R is also very small. Hence the current drawn by the motor is also very small. It will be sufficient to produce the torque.

Synchronous motor on load

Consider a mechanical load is applied to the synchronous motor. A steady increase in load will make the rotor poles fall back a little more relative to the stator poles, as shown below. Hence the torque angle δ increases further with an increase in load.

This increases the resultant voltage E_R which in turn increases the current (I_a = E_R/Z_s) drawn by the motor from the mains.

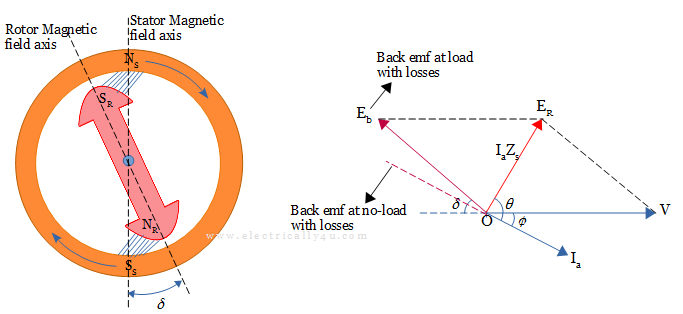
Thus, a synchronous motor is able to supply the necessary torque to the increased mechanical load, by shifting the position of the rotor pole axis with respect to the stator pole axis, maintaining a constant speed or synchronous speed.

Further increase in load will make the induced emf fall back further, which will make the load angle to increase. When the torque angle increases, the voltage E_R increases and does the armature current Ia.

When too much mechanical load is applied to a synchronous motor, the rotor is pulled out of synchronism and comes to a halt or standstill. The maximum torque that a motor can develop without losing its synchronism is called pull-out torque.