Hazards in Digital Circuits | How to eliminate a hazard?

Hazards are the unwanted switching transient that may appear at the output of the digital circuit. Such hazards may result in a malfunction in the output of the circuit.

The propagation delay associated with the logic gates in the circuit is the main cause of hazard. Hazards occur in combinational circuits, which will cause faulty operation. Hazards will also occur in asynchronous sequential circuits where logic gates are used, affecting the stable state.

There are two main types of hazard: Static Hazard and Dynamic Hazard.

Static and Dynamic Hazard

When the input to the logic circuit changes, the output has to remain at a particular logic, but instead it may change its value momentarily. If this happens in the logic circuit, then there exists a static hazard.

The static hazard can be classified as a static-0 hazard and static-1 hazard. Instead of remaining at logic 1, the output goes to logic 0 momentarily, then it is a static-1 hazard. Similarly, if the output monetarily goes to logic 1, instead of remaining at 0, it is a static-0 hazard.

A hazard is said to be dynamic if the output changes two or more times when it should change from 1 to 0 or from 0 to 1.

Illustration of static hazard

Let us consider a logic circuit here. The circuit consists of a NOT gate, two OR gates and an AND gate.

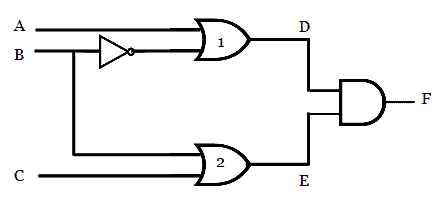
Initially, let us assume the three inputs of the logic circuit as A = B = C =0. This input will cause the output of OR gate 1 to be D = 1 and the output of OR gate 2 to be E = 0. The output of the logic circuit will be equal to F = 0.

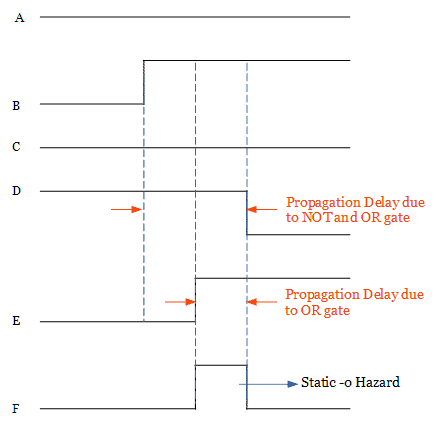
Now if the input B changes from 0 to 1. It will cause the output of gate 1 to be D = 0 and the output of gate 2 to be E = 1. But still, the output of the logic circuit will be equal to F = 0.

While the input B changes from 0 to 1, the delay in the output due to NOT gate and OR gate 1 is more than the delay due to OR gate 2. Due to the lesser delay, the output of gate 2 changes to 1 before the output of gate 1 changes to 0.

At this particular time, both the outputs of gates 1 and 2 will be momentarily equal to 1. Thus the output of the logic circuit will be 1 for a short period of time. In this way, the static-0 hazard will occur in a circuit. The waveform is shown in the figure below.

How to eliminate Hazards in digital circuit?

If a hazard exists in a logic circuit, it is to be eliminated to produce an error-free output. Let us consider a boolean expression F = AB’ + BC. The K-map can be implemented for the given expression, from which the logic circuit is drawn as below.

Learn how to plot the terms in k-map and how to minimize a Boolean expression using K-map.

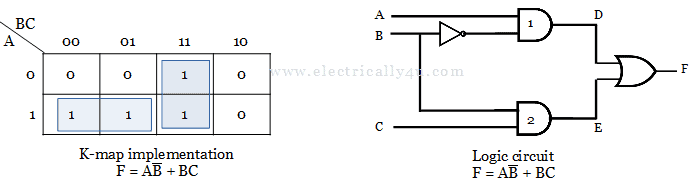
The logic circuit has an inverter and an AND gate, so the delay in the output D is more than that of the output E. So there exists a hazard in the circuit.

With the help of K-map, hazards can be detected in a digital logic circuit. In the k-map, if two adjacent 1’s are not enclosed, then there exists a hazard. To eliminate a hazard, those minterms must be enclosed by introducing another minterm, as shown below.

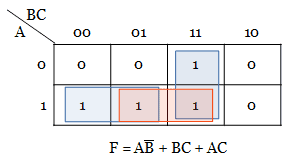
For the obtained expression, the hazard free circuit can be drawn as below.

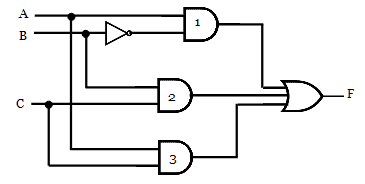
Eliminating Hazards in digital circuit

Now let us consider an example.

Construct a hazard-free logic circuit for a boolean function f(A, B, C, D) = ∑ m(0, 2, 6, 7, 8, 10, 12). For the given expression, let us implement the k-map.

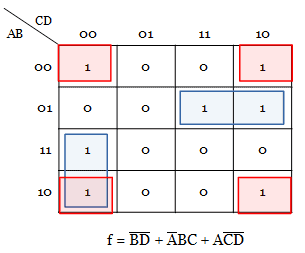
If you observe the above K-map, the minterms AC’D’ and B’D’ are enclosed with each other. But the minterm A’BC is not enclosed with the near group. Thus there exists a hazard.

Now to eliminate the hazard, the minterm A’BC is enclosed with the near minterm by grouping as shown below in green color.

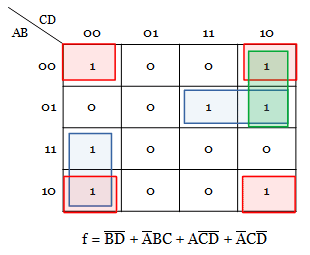
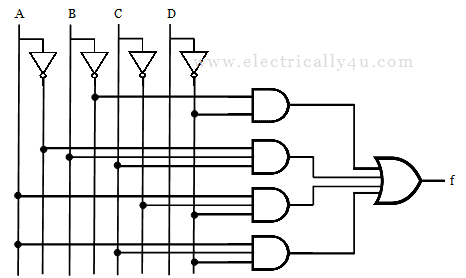
From the minimal expression, draw the hazard free circuit as below