Peak value, Average value and RMS value of AC waveform
As you know, the AC waveform is sinusoidal in nature. Its magnitude continuously varies with time, hence it is necessary to find the value at every instant and its peak value.
Similar to the DC, which has a constant magnitude, we find the average value of an AC quantity, which will also have a constant magnitude. For one complete cycle, you get zero as the average value because it has both positive and negative cycles.
Hence we go for the Root Mean Square(RMS) value, which gives the effective value of a sinusoidal waveform. In this section, you will learn in detail about the instantaneous value, peak value, Average value and RMS value of an AC quantity.
Instantaneous value
At any instant of time, the EMF induced in a coil depends on the rate at which the coil cuts the magnetic flux between the poles. It depends upon the angle of rotation(θ) of the generating device.
Since an AC waveform is continuously changing its magnitude and direction, the waveform at any instant will have a different value from its next instant. For example, the value at 1 millisecond will be different from the value at 1.2 milliseconds and so on. These values are known as Instantaneous Values.
The instantaneous value can be defined as the value of an alternating quantity at any particular instant and is denoted as i and e.
Thus, the instantaneous value of an AC waveform will vary according to the position of the coil within the magnetic field as shown below.
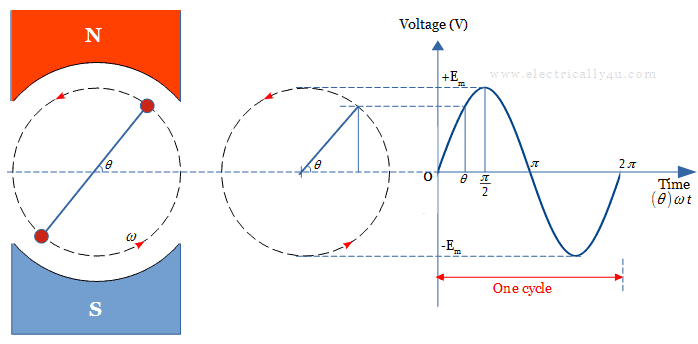
The instantaneous value of a sinusoidal waveform is generalized by the formula.
![]()
![]()
where Em and Im are the maximum values of voltage and current respectively. θ is the angle of rotation of the coil with respect to time.
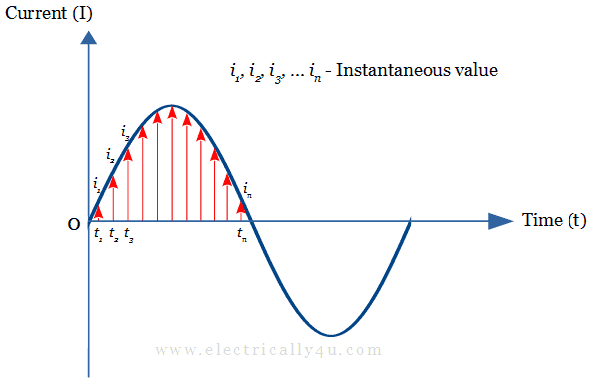
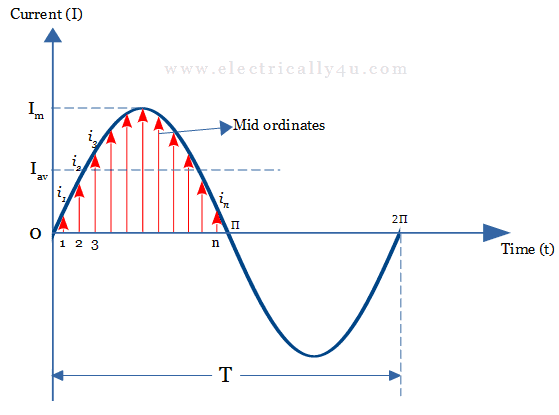
The below figure shows an alternating current waveform, where the instantaneous value of currents i1, i2, i3,… in are marked at different instants t1, t2, t3,… tn respectively. The instantaneous value will be positive(+i) during the positive half cycle and negative(-i) during the negative half cycle.
Peak Value
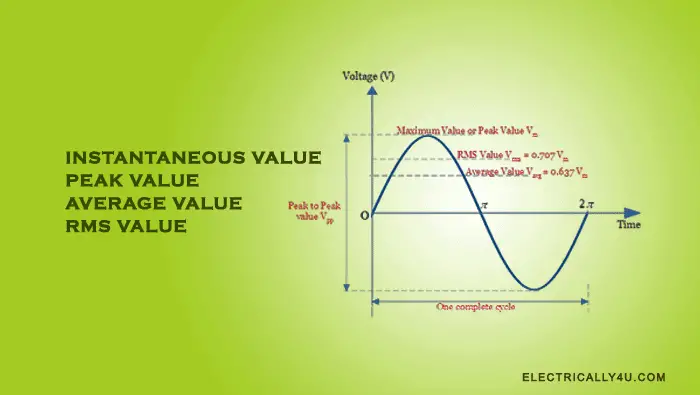
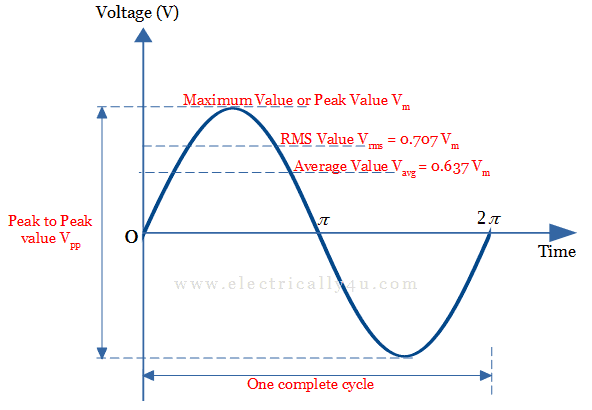
It is the maximum value attained by the AC waveform either in the positive half cycle or negative half cycle. It is also known as amplitude. It is denoted by Im(Ip) for current and Em(Ep) or Vm(Vp) for voltage in the below figure.
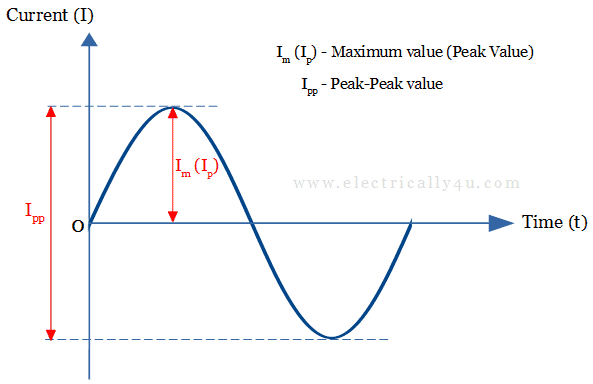
What is peak to peak value?
The sum of peak values of the positive and negative half cycle is known as peak to peak value. It is expressed as Ipp as shown in the above figure.
Mathematically, it is expressed as,
![]()
Check out the calculator to find the Peak to Peak Value of an alternating quantity.
Average value
The average of all the instantaneous value of an alternating quantity over one complete cycle is known as the Average Value. It is expressed as,
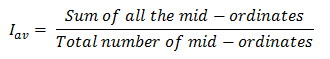
![]()
Here, mid-ordinate represent the different instants of the waveform..
For example, let us consider a sinusoidal waveform, which has 10 mid-ordinates. The instantaneous values i1, i2, i3,… i10 of the alternating current are 2, 4, 6, 8, 10, 8, 6, 4, 2 respectively.
Now, the average value of current is calculated as,
![]()
![]()
The average value of an alternating quantity is also explained as, When we convert the alternating current (AC) into a direct current (DC), then the converted DC value will be the required average value of that alternating current.
Analytical method to find Average value
For one complete cycle, the area under the sinusoidal waveform can be determined by integration as follows,
![]()
Now, the average value of a sinusoidal waveform is obtained by integrating the sinusoidal quantity over a complete cycle and dividing by the total time period(2π).
![]()
![]()
![]()
![]()
![]()
Thus, we found the average value of sinusoidal waveform over one complete cycle is 0. It is zero, because one complete cycle have a positive and negative half cycles.
For a half cycle, the average value of sine wave is obtained by integrating the sinusoidal quantity over a half cycle(0 to π) and dividing by the half time period(π).
![]()
![]()
![]()
![]()
![]()
![]()
Similarly, the average value of voltage is given by,
![]()
Thus, from these equations, we can determine the average value of an alternating quantity, if the maximum or peak value is known.
Check out the calculator to find the Average Value of an alternating quantity.
RMS value
The RMS (Root Mean Square) value is the effective value of an alternating quantity. It means the square root of the mean(average) value of the square of the instantaneous values. The RMS values are denoted by Vrms or Irms.
The RMS value of alternating current is equivalent to the value of direct current (DC) when flowing through a circuit, which produces the same amount of heat, produced by the alternating current (AC) when flowing through the same circuit for a specific time.
In simple words, the effective value is an equivalent DC value that tells you how many volts or amps of DC that a sinusoidal waveform is equal to in terms of its ability to produce the same power.
Graphically, the RMS value of an alternating quantity can be expressed as,
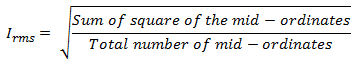
![Rendered by QuickLaTeX.com \[{I_{rms}=\sqrt{\left(\frac{I_1^2 + I_2^2 + I_3^2 + ... + I_n^2}{n}\right)}\]](https://www.electrically4u.com/wp-content/ql-cache/quicklatex.com-eb5f13b6334a6632614fc19e0a6599c2_l3.png)
Analytical Method to find RMS value
Analytically, the integration is done to the squared function of the instantaneous value of sinusoidal quantity over a complete cycle(0 to 2π) and divide it by the total time period(2π), to get the mean value.
Now the RMS value is obtained by taking the square root of the entire function.
![Rendered by QuickLaTeX.com \[{I_{rms}=\sqrt{\left(\frac{1}{2\pi}\int_0^{2\pi}i^2\,\mathrm{d}\theta\right)\]](https://www.electrically4u.com/wp-content/ql-cache/quicklatex.com-7f352d0e12cfde6ea4c81a522c27c0ec_l3.png)
![Rendered by QuickLaTeX.com \[{I_{rms}=\sqrt{\left(\frac{1}{2\pi}\int_0^{2\pi}I_m^2 sin^2 \theta\,\mathrm{d}\theta}}\right)\]](https://www.electrically4u.com/wp-content/ql-cache/quicklatex.com-889b6c25607b0f498acb91093113bd50_l3.png)
![Rendered by QuickLaTeX.com \[{I_{rms}=\sqrt{\left(\frac{I_m^2}{2\pi}\int_0^{2\pi} sin^2 \theta\,\mathrm{d}\theta}}\right)\]](https://www.electrically4u.com/wp-content/ql-cache/quicklatex.com-f48a59d36ee90ce9b91ccb66ea2ae8de_l3.png)
Here,
![]()
Therefore, RMS value of current becomes,
![Rendered by QuickLaTeX.com \[{I_{rms}=\sqrt{\left(\frac{I_m^2}{2\pi}\int_0^{2\pi} \frac{1-cos2\theta}{2}\,\mathrm{d}\theta}}\right)\]](https://www.electrically4u.com/wp-content/ql-cache/quicklatex.com-6868dd7ed995bb7e1e1475532676982e_l3.png)
![Rendered by QuickLaTeX.com \[{I_{rms}=\sqrt{\left(\frac{I_m^2}{4\pi}\left[\theta-\frac{sin2\theta}{2}\right]_0^{2\pi}}\right)\]](https://www.electrically4u.com/wp-content/ql-cache/quicklatex.com-451f3040456aaef8e130aeee4c98f5e4_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\boxed{I_{rms}=\sqrt{\frac{I_m^2}{2} } = 0.707 I_m}\]](https://www.electrically4u.com/wp-content/ql-cache/quicklatex.com-c24ab9ff44fb13ab2e144b73c7232247_l3.png)
Similarly, the RMS value of voltage is given by,
![Rendered by QuickLaTeX.com \[\boxed{V_{rms}=\sqrt{\frac{V_m^2}{2} } = 0.707 V_m}\]](https://www.electrically4u.com/wp-content/ql-cache/quicklatex.com-389649fbe47aabd12cfd07fec99258c3_l3.png)
Check out the calculator to find the RMS Value of an alternating quantity.
The Generalized AC waveform representing the peak value, average value and RMS value is shown below,
Form Factor
The ratio between the RMS value and the average value of an alternating quantity is known as the Form Factor. For a pure sinusoidal waveform, the value of the form factor will always be equal to 1.11
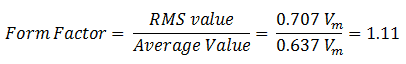
Peak Factor
Peak Factor is defined as the ratio of maximum(peak) value to the RMS value of an alternating quantity. For a pure sinusoidal waveform, the peak Factor will always be equal to 1.414. The peak factor is also called as crest factor.
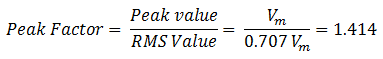


Related Posts