AC resistance and impedance

AC resistance and DC resistance are the opposition offered to the flow of AC and DC currents respectively through a conductor. However, in AC circuits, the resistance is called impedance.

Impedance is the effective resistance offered to the current flow around a circuit containing resistance, inductive reactance, and capacitive reactance. It is measured in Ohms.

As you know, in an AC circuit, the voltage and current phasors are represented mathematically in a complex form. The sinusoidal waveforms that are in the time-domain form can be converted into the spatial or phasor-domain so that phasor diagrams can be constructed to find this phasor voltage-current relationship.

Any ideal circuit element such as a resistor, inductor, or capacitor can be described mathematically in terms of its voltage and current.

AC Resistance with a Sinusoidal Supply

In general, the voltage across a pure ohmic resistor is linearly proportional to the current flowing through it, as defined by Ohm’s Law.

Consider the circuit as shown below. It consists of an AC voltage source V, a switch, and a load resistor R.

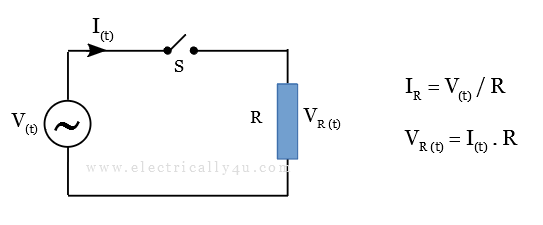
When the switch is closed, the AC voltage is applied to the resistor. This voltage will cause a current to flow through the circuit. The voltage drop across the load resistor R is V_R(t).

Since the applied voltage is alternating, it rises and falls sinusoidally. Simultaneously, the current flowing through the circuit will also rise and fall.

In other words, with AC resistance, the voltage and current reach their maximum values and fall through zero at the same time and are therefore said to be in phase with each other.

The electric current that flows through an AC resistance is represented by the expression, 

   

where I_m is the peak amplitude of the current and θ is the phase angle between voltage and current.

By Ohm’s law, the maximum voltage or peak voltage across the terminals of R will be given by,

   

and the instantaneous value of the current, I_(t) will be

   

Thus for a purely resistive circuit, the AC current flowing through the resistor varies in proportion to the applied voltage, following the same sinusoidal pattern. As the supply frequency is the same for both voltage and current, their phasors lie on the same line, resulting in the current being “in phase” with the voltage.

That is, there exists there is no phase difference between the current and the voltage when using an AC resistance. It is because both voltage and current will reach its maximum, zero, and minimum values simultaneously.

Impedance

In a DC circuit, the voltage-current relationship is commonly called Resistance, but in an AC circuit, this relationship is called Impedance.

In other words, the electrical resistance in an AC circuit is called “Impedance”. We can say that for a resistor, DC resistance = AC impedance(R = Z).

Impedance is represented by the symbol ‘Z‘. The unit of AC resistance or impedance is Ohm(Ω), which is the same as DC resistance.

The Impedance (or AC resistance) can be defined as

   

Impedance can also be represented by a complex number as it depends upon the frequency of the circuit, ω when reactive components are present.

But in the case of a purely resistive circuit, the reactive component will always be zero. Thus the general expression for impedance in a purely resistive circuit in terms of a complex number is given as,

   

Waveforms and phasor diagram of AC Resistance

The waveforms of voltage and current in the AC resistance is shown below. The “in-phase” relationship can be clearly seen in the phasor diagram.

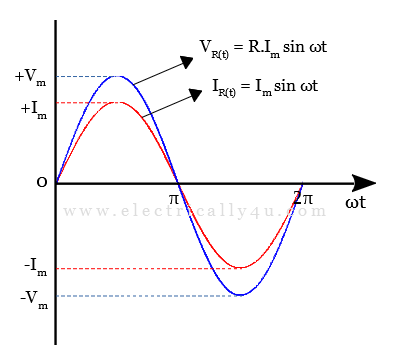
In the complex domain, resistance is just a real number, it does not include an imaginary component. Hence, the vectors of both voltage and current lie on the same line. It means there will be no phase difference ( θ = 0 ) between them or both in-phase with each other.

Thus the phasors of both voltage and current are drawn super-imposing with each other along the reference axis. The sinusoidal time-domain diagram is transformed into the phasor-domain as below.

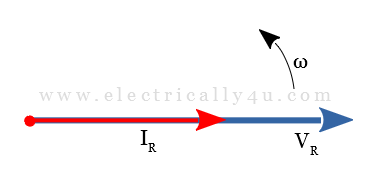
Voltage and Power relationships

The above phasor represents the RMS values of voltage and current through the resistance. The RMS values are given by,

   

   

The phase voltage and current relationship is given as,

   

   

This shows that a pure resistance within an AC circuit produces a relationship between its voltage and current phasors in exactly the same way as that of a DC circuit. Ohm’s law is applicable to both AC and DC circuits. In both cases, the voltage-current relationship is always linear for pure resistance.

The power consumed by the resistor in an AC circuit depends upon the phase angle. It is given as,

   

But in a purely resistive circuit, the phase angle θ = 0. So, the AC power becomes,

   

The above equations are the same as that of DC circuits. Thus we can say that the effective power consumed by an AC resistance is equal to the DC power consumed by the same resistor in a DC circuit.

It is possible to apply basic laws such as Ohm’s law and Kirchhoff’s law to find the voltage, current, and Impedance in an AC circuit similar to that of a DC circuit.

Examples of pure resistances are heating elements and lamps, which have negligible values of inductance or capacitance.

Example Problem

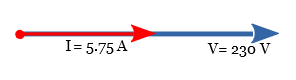
An electrical lamp that has a resistance of 40 Ohms is connected across a 230V AC single-phase supply. Calculate the current drawn from the supply and the power consumed by the lamp. Also, draw the corresponding phasor diagram.

Solution:

Given: Voltage = 230 V, Lamp resistance = 40 Ohms

Current drawn from the supply,

   

The power consumed by the lamp, 

   

Since it is a resistive load, there is no phase difference, thus θ = 0. The corresponding phasor diagram is drawn as below