Programmable Array Logic(PAL)

Programmable Array Logic (PAL) is a logic device, which has programmable AND array and fixed OR array. It is used to realize a logic function.
In this PLD, only AND gates are programmable and hence it is easier to work with PAL. But when compared to the Programmable Logic Array(PLA) Device, it is not as flexible as PLA, as the programming part is limited to AND array.
Block diagram of Programmable Array Logic
The block diagram of PAL is given below. It has n inputs and m outputs. Each input has a buffer gate and an inverter gate. Buffer gate is added to the normal input, NOT gate is added to the inverted or complemented input.
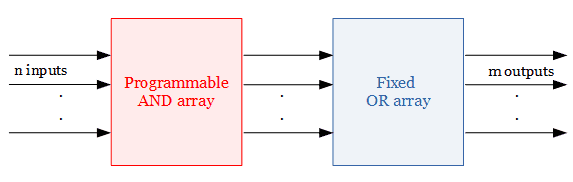
The following figure shows the internal structure of Programmable Array Logic. The product terms can be programmed through the fuse link.
It means the user can decide the connection between the inputs and the AND gates. If a particular input line is to be connected to the AND gate, then the fuse link must be placed at the interconnection.
The AND gate outputs are then fed as an input to the fixed OR gate. Depending upon the required function, the output line of the AND gate is connected to the corresponding input of the OR gate.
The output thus produced will be the realization of the logic function in sum of product(SOP) form.
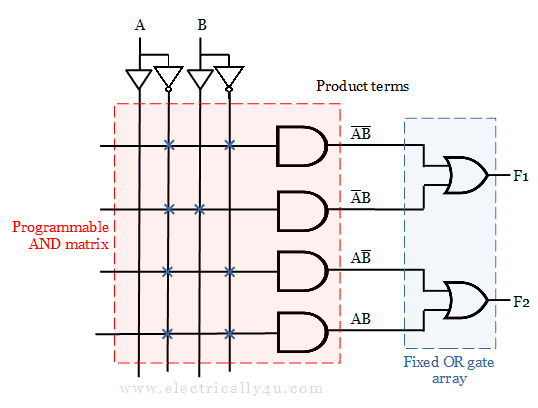
Now, lets look at some of the examples here.
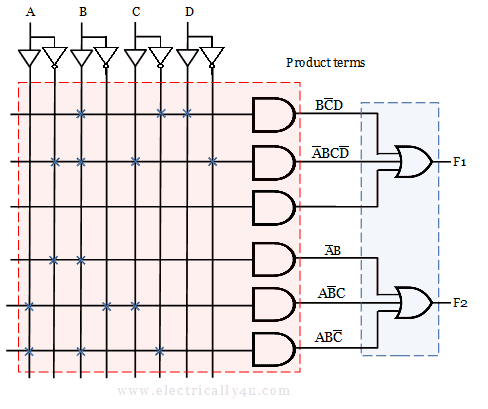
Solved Example 1
Implement the Boolean functions F1 = A’BC’D + A’BCD’ + ABC’D and F2 = A’BC’ + A’BC + AB’C + ABC’ with PAL device.
The given Boolean expressions can be simplified to get a reduced equation.
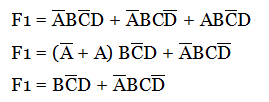
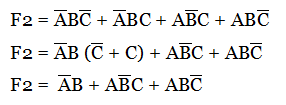
The simplified expression can be realized using PAL. The given function has four inputs and two outputs.
The simplified expression has five product terms. Each product term is obtained by placing the fuse link to the corresponding input line.
Solved Example 2
Any type of combinational circuit can be realized using PAL. In this example, let’s see how a BCD to Gray code converter is realized using PAL.
For this realization, the code conversion must be done, which you can refer from code converters.
From the truth table, the following four Sum of Product terms are obtained using Karnaugh Map method.
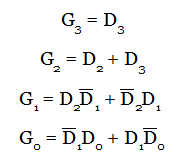
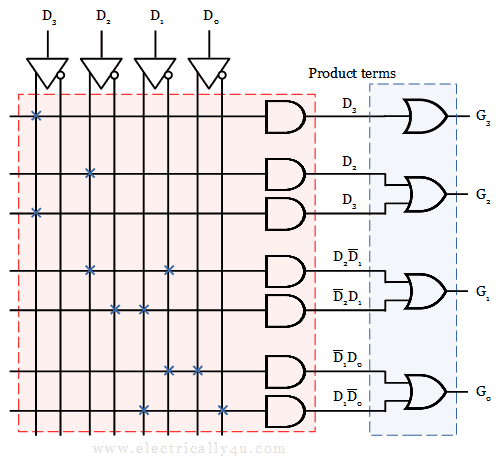
Now, the logic circuit for the above SOP expressions can be implemented using PAL. It will have four BCD inputs and four gray code outputs.


Related Posts