EMF equation of alternator

The emf induced by the alternator or synchronous generator is three-phase alternating in nature. Let us derive the mathematical equation of emf induced in the alternator.
Let,
Z = number of conductors in series per phase.
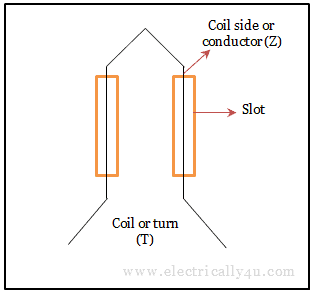
Z = 2T, where T is the number of coils or turns per phase. One turn has two coil sides or conductor as shown in the below diagram.
P = Number of poles.
f = frequency of induced emf in Hertz
Φ = flux per pole in webers.
Kp = pitch factor, Kd = distribution factor,
Kf = Form factor
N = Speed of the rotor in rpm(revolutions per minute)
N/60 = Speed of the rotor in revolutions per second.
Time taken by the rotor to complete one revolution,
dt = 1/(N/60)= 60/N second
In one revolution of the rotor, the total flux Φ cut the by each conductor in the stator poles, dΦ = ΦP weber
By faraday’s law of electromagnetic induction, the emf induced is proportional to rate of change of flux.

We know, the frequency of induced emf
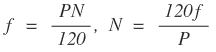
Submitting the value of N in the induced emf equation, We get

If there are Z conductors in series per phase,
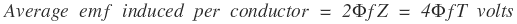
RMS value of emf per phase = Form factor x Average value of induced emf = 1.11 x 4 Φ f T
RMS value of emf per phase = 4.44 Φ f T volts
The obtained above equation is the actual value of the induced emf for full pitched coil or concentrated coil. However, the voltage equation gets modified because of the winding factors.
Actual induced emf per phase = 4.44 Kp Kd Φ f T volts = 4 Kf Kp Kd Φ f T volts
Solved Problem
Let us solve a problem on the above emf equation.
A 3 phase, 16 pole alternator has a star-connected winding with 144 slots and 10 conductors per slot. The flux per pole is 0.02 Wb, sinusoidally distributed and the speed is 375 rpm. Find the frequency of the induced emf, phase emf and line emf. Assume the coil as full pitched.
Given parameters: P = 16, slots = 144 , Z = 10 conductors per slot, Φ = 0.02 wb, N = 375 rpm, for full pitch coil, Kp = 1.
To find : f, Eph, EL
Solution:
f= PN/120 = 16 x 375/120,
f = 50 Hz
The emf equation of alternator is given by, Eph= 4.44 Kp Kd Φ f T volts
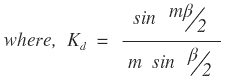
Here, m = no. of slots/pole/phase = 144/16/3 = 3
where n=no. of slots/pole = 144/16 = 9
![]()
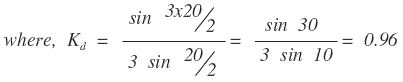
Z = 10 conductors per slot per phase = 10 x 144/3 = 480
T = Z/2 = 480 /2 = 240
Eph= 4.44 x 1 x 0.96 x 0.02 x 50 x 240 = 1022.97 V
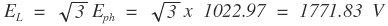





good one
Wow! Nice derivation
Nice derivation