Series and Parallel combination of Capacitor
Capacitor is a passive element, in which the energy is stored in the form of electrostatic field. This property of capacitor is called as capacitance. The unit of capacitance is Farad(F), which was named after the British Scientist Michael Faraday.
If V is the voltage applied to the capacitor and q is the charge stored, then the value of capacitance is given by,
![\[ C = \frac{q}{V}\]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-22e853b08ebf55d2d7dc8e709529c587_l3.png "Rendered by QuickLaTeX.com")
Capacitor in series
Consider three capacitors C1, C2 and C3 that are connected in series. Let V be the voltage supply that is connected to the series capacitors and I be the current flowing from the supply. Here, each capacitor carries an equal amount of charge q.
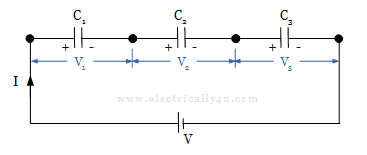
The voltage drops across each capacitor be V1, V2 and V3. So the total voltage V is given by V = V1 +V2 + V3.
Across each capacitor, the potential difference is given by,
![\[ V_1 = \frac{q}{C_1}, V_2 = \frac{q}{C_2}, V_3 = \frac{q}{C_3}\]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-ff8c53a3e7c3922d52a70e154c184a7f_l3.png "Rendered by QuickLaTeX.com")
Thus the resultant voltage is
![\[ V = \frac{q}{C_1} + \frac{q}{C_2} + \frac{q}{C_3} = q(\frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3}) --->(1)\]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-4dada1c20f3228e59cbd040d71b23be5_l3.png "Rendered by QuickLaTeX.com")
If Cs is the effective capacitance of the series combination, then the voltage V is given by,
![\[V = \frac{q}{C_s} --->(2)\]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-795894cb2294351d19a64f75998c0812_l3.png "Rendered by QuickLaTeX.com")
From (1) and (2),
![\[\frac{1}{C_s} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-2e4acec7d9b4fea248c117b94c6ea268_l3.png "Rendered by QuickLaTeX.com")
If there are ‘n’ number of capacitors connected in series, then the equivalent capacitance value is given by
![\[\frac{1}{C_s} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} + ... \frac{1}{C_n} \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-d4ae5182236d87375afe9af1de59df80_l3.png "Rendered by QuickLaTeX.com")
Capacitors is parallel
Let us consider three capacitors C1, C2 and C3 connected in parallel. Let V be the supply voltage and I be the current flowing from the supply.
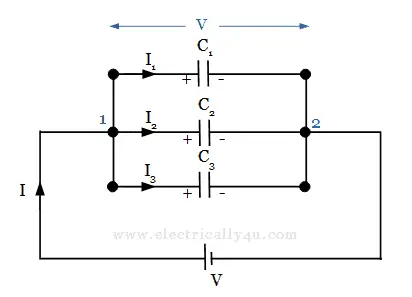
For parallel capacitors, the voltage across each capacitor is the same. Thus the charge on the three capacitors is given by
![\[ q_1 = {C_1}{V}, q_2 = {C_2}{V}, q_3 = {C_3}{V}\]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-f7ee0f963c976486316a8672fbed6479_l3.png "Rendered by QuickLaTeX.com")
The total charge in all the capacitor is
![\[q = q_1 + q_2 + q_3 = {C_1}{V} + {C_2}{V} + {C_3}{V} --->(3) \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-3144864dd4975fbdd60949ce868a6684_l3.png "Rendered by QuickLaTeX.com")
The effective capacitance of the circuit is given by,
![\[q = C_pV --->(4)\]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-4727b075b8ab955a6f0281e7b037c001_l3.png "Rendered by QuickLaTeX.com")
From equations (3) and(4),
![\[C_pV = {C_1}{V} + {C_2}{V} + {C_3}{V} = V(C_1 + C_2 + C_3)\]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-f617825254a641064a9871ecaa537f86_l3.png "Rendered by QuickLaTeX.com")
![\[C_p = C_1 + C_2 + C_3\]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-146b4ccd32894dff2eff43d04d098b74_l3.png "Rendered by QuickLaTeX.com")
If there are ‘n’ number of capacitors connected in parallel, then the effective capacitance is given by
![\[C_p = C_1 + C_2 + C_3 + ... + C_n\]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-9fcb8d14316b85128d51f88f3ff9f60b_l3.png "Rendered by QuickLaTeX.com")
Hence the effective capacitance of the capacitors connected in parallel is the sum of the capacitances of the individual capacitors.
For example, if a capacitor of 0.6 μF is connected in series with the parallel combination of three capacitors with capacitances 0.2 μF, 0.4 μF and 0.7 μF, then how to determine the effective capacitance of the circuit.
In the given problem, C1 =0.6μF is in series with the parallel combination of C2 = 0.2 μF, C3 = 0.4 μF, C4 = 0.7 μF.
Cp = C2 + C3 + C4 = 0.2 + 0.4 + 0.7 = 1.3 μF.
![\[\frac{1}{C_{eff}} = \frac{1}{C_1} + \frac{1}{C_p} = \frac{1}{0.6} + \frac{1}{1.3} = 2.43 \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-57315895d8a82728ddeba8ca1c3ad391_l3.png "Rendered by QuickLaTeX.com")
Ceff = 0.411 μF
Related Posts