Transformer with winding resistance and leakage reactance

Resistance of transformer

An ideal transformer has no losses because it possesses no resistance. It is not possible to build an ideal transformer. But an actual transformer always has some resistance in the primary and secondary windings. Due to this resistance, there is some voltage drop in the two windings.

The result is that the EMF induced in the primary winding E₁ is less than the primary input voltage. It is because of the resistance R₁ in the primary winding. The equation becomes

   

The secondary terminal voltage V_₂ is vectorially less than the secondary induced e.m.f. E₂ because of the resistance R₂ of the secondary winding. Hence, V₂ becomes

   

Leakage Flux in transformer

For an ideal transformer, it was assumed that the entire flux developed by the primary winding, links with every turn of both the primary and secondary windings. But in practice, it is not possible to realize this condition.

However, part of the flux Φ_L1 set up by the primary winding links only with the primary turns, as illustrated in the figure below. Also, some of the flux Φ_L2 set up by the secondary winding links only the secondary turns.

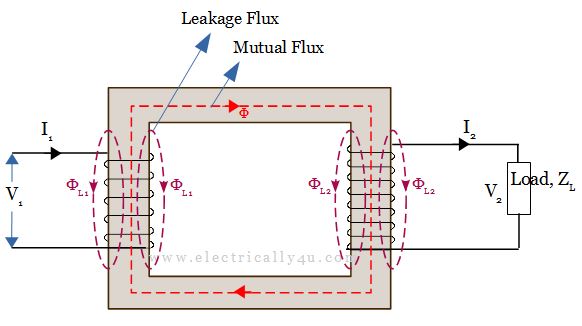
These two fluxes Φ_L1 and Φ_L2 are known as leakage flux. It is defined as the flux that leaks out of the core and does not link both windings.

The primary leakage flux Φ_L1 is proportional to the primary current and the number of primary turns being fixed.

Leakage Reactance of transformer

On no load, the primary current is so small that the leakage flux produced by it can be neglected. Under load conditions, primary current increases resulting in an increase in ampere-turns, and hence leakage flux increases.

The primary leakage flux Φ_L1 is in phase with I₁ and produces self-induced emf E_L1 given by E_L1=2πfL₁I₁ in the primary winding, where L₁ is the self-inductance of the primary winding produced by primary leakage flux Φ_L1.

The self-induced emf E_L1 due to primary leakage flux in the primary winding will lag the leakage flux Φ_L1 and primary current I₁ by 90°. This emf is nothing but the reactance voltage and is denoted by I₁X₁.

The effect of the primary leakage flux, therefore, is to induce an emf that opposes the flow of current through the transformer. The reactance of the primary winding X₁ is written below as.

   

Similarly, when the transformer is operated on load, secondary current I₂ flows through the secondary winding, which produces its own flux Φ₂. A part of this flux will leak out of the core, called secondary leakage flux Φ_L2, which is in phase with the secondary current I₂.

This leakage flux produces self-induced emf E_L2 = 2πfL₂I₂ in the secondary winding where L₂ is self-inductance of secondary winding due to leakage flux Φ_L2.

This emf is also called a reactance voltage I₂X₂ which lags the secondary current I₂ by 90º, where X₂ is the secondary reactance and is given as,

   

A transformer with winding resistance and leakage reactance is equivalent to an ideal transformer having inductive and resistive coils connected in series with each winding as shown below.

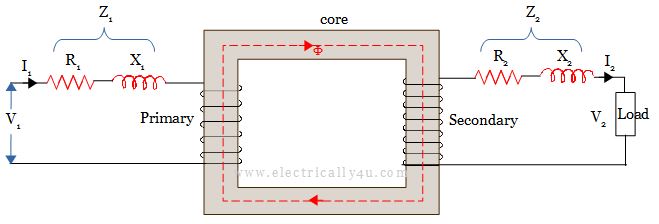
Impedance of Transformer

As discussed above, both primary and secondary windings will have resistance and leakage reactance. The combination of both resistance and reactance is nothing but the impedance of the transformer. If R₁ and R₂ are primary and secondary resistances, X₁ and X₂ are leakage reactances of the transformer respectively, then Z₁ and Z₂ are the impedance of primary and secondary windings. The equations of impedances are given by,