Transformer on load condition

A transformer is said to be on load when the primary is connected to the alternating voltage source and its secondary is connected to the load. When a transformer is operated at no load condition, the current from the secondary winding to the load will not flow.

But when the transformer is connected to the load, the secondary current flows from the winding to the load. Let us now look at what happens, when the load is connected to the transformer.

Operation of Transformer on load condition

When the secondary circuit of a transformer is connected through an impedance or load, the transformer is said to be loaded. The current I₂ is set up in the secondary winding that flows through the load.

The magnitude and phase of this secondary current I₂ with respect to secondary terminal voltage V₂ will depend upon the characteristics of the load, i.e., resistive, inductive, and capacitive.

If the load is resistive, the current I₂ will be in-phase with V₂. Similarly the current will lag behind and lead the terminal voltage if the load is inductive and capacitive respectively.

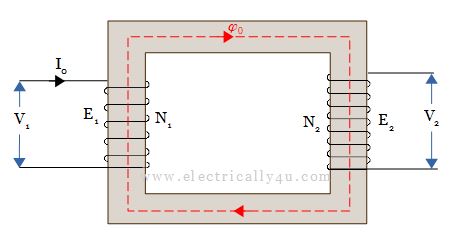
When the transformer is on no load, as shown in the above figure, it draws no-load current I₀, from the supply mains. The no-load current I₀ sets up an MMF (N₁I₀), which produces flux Φ₀ in the core.

When an impedance is connected across the secondary terminals, as shown in the Figure below, current I₂ flows through the secondary winding. The secondary current I₂ sets up its own MMF(N₂I₂) and hence creates a secondary flux Φ₂.

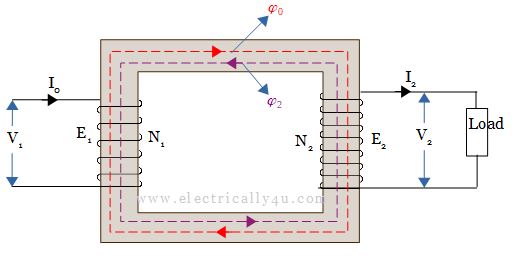
The secondary flux Φ_₂ opposes the main flux set up by the exciting current I₀, according to Lenz’s law. The opposing secondary flux Φ₂ weakens the main flux momentarily, so primary back emf E₁ tends to be reduced.

At this period, the applied voltage V₁ will be more than the back emf E₁. Thus the primary winding draws more current from the supply. It again causes an increase in back emf E₁, and it adjusts itself such that there is a balance between applied voltage V_₁ and back emf E_₁.

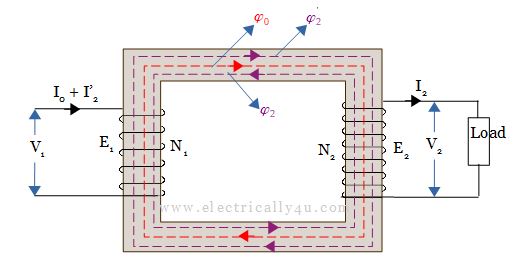
Let the additional primary current be I’₂, called as load component of the primary current. The current I’₂ is in phase opposition with secondary current I₂ and is also called the counter-balancing current.

The additional current I’₂ in the primary winding sets up an MMF (N₁I’₂) producing flux Φ’₂ in the same direction as that of the main flux Φ₀. It cancels the flux Φ_₂ produced by secondary MMF (N_₂I₂) being equal in magnitude.

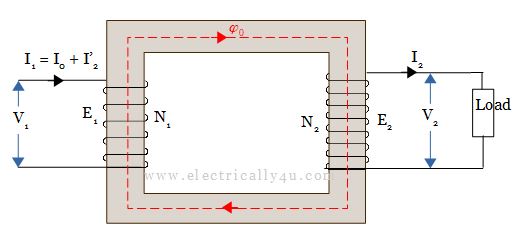
Hence during the load condition, only the main flux exists in the transformer core. Therefore, whatever might be the load condition, the flux passing through the core is almost constant as that of no load condition.

As Φ_₂ = Φ’₂

   

   

When the transformer is on load, the primary winding has two currents.

• No load current I₀
• Counterbalancing or load component of primary current I’₂

Thus the total primary current I₁ is the phasor sum of both currents I₀ and I’₂.

   

Since the no-load current is very small compared to I’₂, the total primary current is approximately equal to I’₂

   

   

where K is called the transformation ratio.

From equation(2), it can be understood that the primary and secondary currents are inversely proportional to their respective turns.

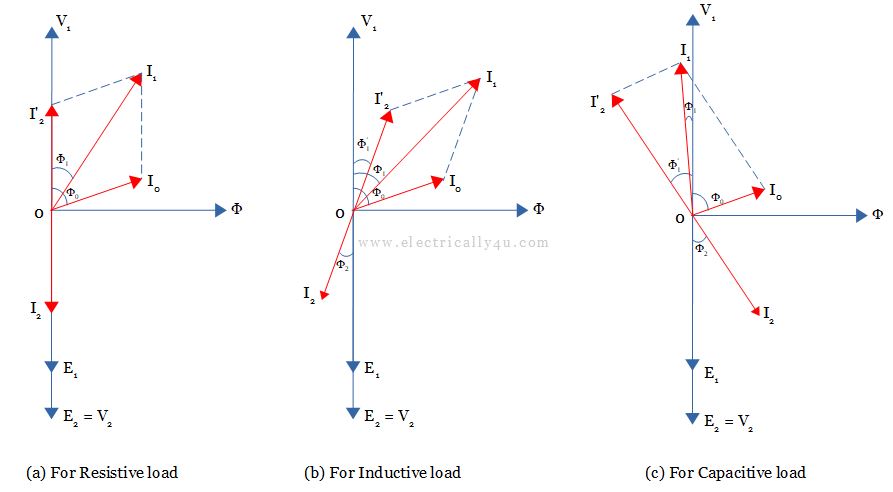
Phasor diagram of a transformer on load

The phasor diagram of a transformer on load is drawn below for resistive, inductive, and capacitive loads. To draw the phasor diagram,

• Let us consider the flux Φ₀ as the reference phasor.
• Draw the V₁ phasor leading the flux Φ₀ by 90⁰.
• Draw the induced EMFs E₁ and E₂ phasor opposite to the voltage phasor V₁.
• Draw the no-load primary current I₀ by lagging V₁ by an angle Φ₀.
• Draw the secondary current I₂.
• For different load conditions,
  • Resistive Load – I₂ is drawn in phase with V₂.
  • Inductive Load – I₂ is drawn lagging V₂ by an angle Φ₂.
  • Capacitive Load – I₂ is drawn leading V₂ by an angle Φ₂.
• Draw the load component of primary current I’₂, opposite and equal to the current phasor I₂.
• Draw the primary current I₁ lagging the voltage phasor V₁ by an angle Φ₁. I1 is also the vector sum of I₀ and I’₂.